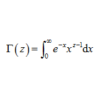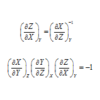力のモーメントの計算

問題

以下の図に力$\vec{F}$が作用した場合の力のモーメント$\vec{M}$を計算し、力のモーメントの大きさ$|\vec{M}|$を求めよ。但し、棒の質量は無視できるものとする。

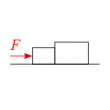
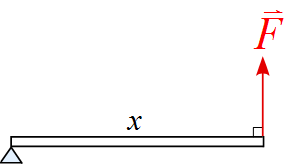
(1) 棒の長さ$x, \ $棒と作用する力は直交する場合。

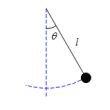
(2) 棒の長さ$x, \ $棒と作用する力のなす角は$\theta$の場合。

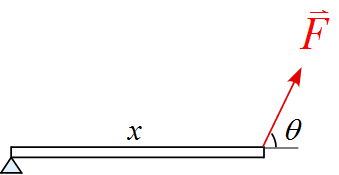
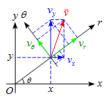
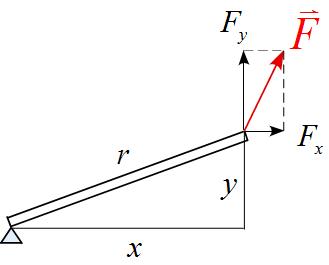
(3) 棒の長さ$r, \ $作用する力$\vec{F}$の$x,y$成分を$F_x ,\ F_y $とする場合。

解答

(1)
位置ベクトル$\vec{r}_1$を図のように設定すると、

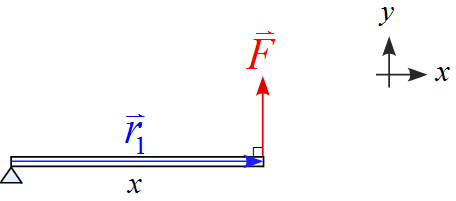
位置ベクトルは
\begin{eqnarray*}
\vec{r}_{1} &=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}

である。
また、作用する力は

\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
0 \\
F \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。

従って、力のモーメント$\vec{M}_1$は

\begin{eqnarray*}
\vec{M}_{1} &=& \vec{r}_{1} \times \vec{F} \\
\\
&=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0\\
F\\
0\\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \cdot 0 -0 \cdot F \\
0 \cdot 0 – x \cdot 0 \\
x \cdot F – 0 \cdot 0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
xF \\
\end{pmatrix}\\
\end{eqnarray*}

となり、

\begin{eqnarray*}
| \vec{M}_{1} | &=& \sqrt{0^2 + 0^2 + (xF)^2} \\
\\
&=& xF
\end{eqnarray*}

となる。

(2)
位置ベクトル$\vec{r}_2$を図のように設定すると、

位置ベクトルは
\begin{eqnarray*}
\vec{r}_{2} &=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}

である。
また、作用する力は

\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
F \cos \theta \\
F \sin \theta \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。

従って、力のモーメント$\vec{M}_2$は

\begin{eqnarray*}
\vec{M}_{2} &=& \vec{r}_{2} \times \vec{F} \\
\\
&=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
F \cos \theta \\
F \sin \theta \\
0\\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \cdot 0 -0 \cdot F \sin \theta \\
0 \cdot F \cos \theta – x \cdot 0 \\
x \cdot F \sin \theta – 0 \cdot F \cos \theta \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
xF \sin \theta \\
\end{pmatrix}\\
\end{eqnarray*}

となり、

\begin{eqnarray*}
| \vec{M}_{2} | &=& \sqrt{0^2 + 0^2 + (xF \sin \theta)^2} \\
\\
&=& xF \sin \theta
\end{eqnarray*}

となる。

(3)
位置ベクトル$\vec{r}_3$を図のように設定すると、

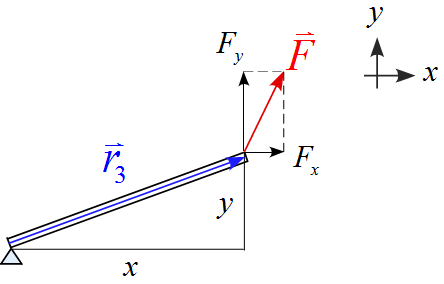
位置ベクトルは
\begin{eqnarray*}
\vec{r}_{3} &=&
\begin{pmatrix}
x \\
y \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}

である。
また、作用する力は

\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
F_x \\
F_y \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。

従って、力のモーメント$\vec{M}_3$は

\begin{eqnarray*}
\vec{M}_{3} &=& \vec{r}_{3} \times \vec{F} \\
\\
&=&
\begin{pmatrix}
x \\
y \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
F_x \\
F_y \\
0\\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
y \cdot 0 -0 \cdot F_y \\
0 \cdot F_x – x \cdot 0 \\
x \cdot F_y – y \cdot F_x \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
xF_y – yF_x \\
\end{pmatrix}\\
\end{eqnarray*}

となり、

\begin{eqnarray*}
| \vec{M}_{3} | &=& \sqrt{0^2 + 0^2 + (xF_y – yF_x )^2} \\
\\
&=& xF_y – yF_x
\end{eqnarray*}

となる。