単振り子の運動

問題

質量$m$の物体が長さ$l\ $の糸につるされている。
この物体の単振り子運動について以下の問いに答えよ。

(1) 極座標を考えたとき、$r$方向と$\theta$方向の運動方程式を立てよ。

(2) 振れ角$\theta$が十分に小さいとき$\sin\theta\simeq\theta$が成立する。
$\ \ \ \ \ $この時の運動の周期$T$を求めよ。

(3) 物体を十分小さな角$\theta_0$の地点から$t=0$で運動させたとする。
$\ \ \ \ \ $この運動に置いて振れ角$\theta(t)$と糸の張力$S$を求めよ。

解答

(1) 物体に作用する力を書き込むと、

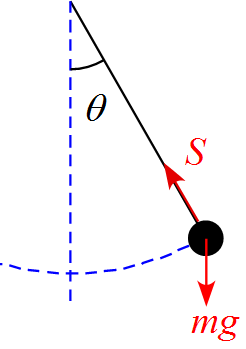
物体に作用する力は重力$mg$と張力$S$である。
これらの力を$r$方向と$\theta$方向の成分に分解すると

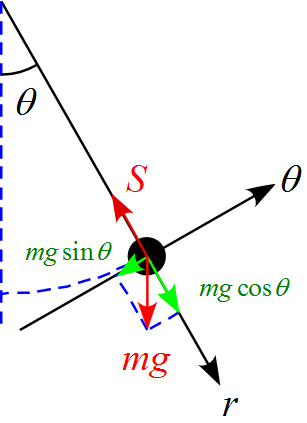
となる。
よって運動方程式は、
\begin{align*}
\begin{cases}
ma_r=mg\cos\theta-S\\
ma_\theta=-mg\sin\theta
\end{cases}
\end{align*}
となる。
ここで、極座標において

\begin{align*}
a_r&=\frac{\diff^2 r}{\diff t^2}-r\left(\frac{\diff\theta}{\diff t}\right)^2\\
a_\theta&=2\frac{\diff r}{\diff t}\frac{\diff\theta}{\diff t}+r\frac{\diff^2\theta}{\diff t^2}
\end{align*}

であり、糸は伸び縮みせず、$r=l$、$\frac{\diff r}{\diff t}=0$であるから
\begin{align*}
ma_r&=mg\cos\theta-S\\
m\left[\frac{\diff^2 r}{\diff t^2}-l\left(\frac{\diff\theta}{\diff t}\right)^2\right]&=mg\cos\theta-S\\
-ml\left(\frac{\diff\theta}{\diff t}\right)^2&=mg\cos\theta-S\\
ml\left(\frac{\diff\theta}{\diff t}\right)^2&=S-mg\cos\theta\\
ma_\theta&=-mg\sin\theta\\
m\left[2\frac{\diff r}{\diff t}\frac{\diff\theta}{\diff t}+l\frac{\diff^2\theta}{\diff t^2}\right]&=-mg\sin\theta\\
ml\frac{\diff^2\theta}{\diff t^2}&=-mg\sin\theta
\end{align*}
従って、
\begin{align*}
\begin{cases}
ml\left(\frac{\diff\theta}{\diff t}\right)^2=S-mg\cos\theta\\
ml\frac{\diff^2\theta}{\diff t^2}=-mg\sin\theta
\end{cases}
\end{align*}
となる。

(2) $\sin\theta\simeq\theta$とすると、
\begin{align*}
ml\frac{\diff^2\theta}{\diff t^2}&=-mg\sin\theta\\
ml\frac{\diff^2\theta}{\diff t^2}\simeq&-mg\theta\\
\frac{\diff^2\theta}{\diff t^2}&=-\frac{g}{l}\theta
\end{align*}
よって
\begin{align*}
\theta=A\cos\theta(\omega t+\phi)\\
\mbox{（但し、$\omega^2=\frac{g}{l},A,\phi$は定数）}
\end{align*}
となる。
従って周期$T$は
\begin{align*}
T=\frac{2\pi}{\omega}&=\frac{2\pi}{\sqrt{\frac{g}{l}}}\\
&=2\pi\sqrt{\frac{l}{g}}
\end{align*}
となる。

(3) この運動において
\begin{align*}
\theta&=A\cos(\omega t+\phi)\\
\frac{\diff\theta}{\diff t}&=-A\omega\sin(\omega t+\phi)
\end{align*}
である。
初期条件より
\begin{align*}
\theta(0)&=\theta_0\\
\frac{\diff\theta(0)}{\diff t}&=-A\omega\sin(\omega\cdot0+\phi)=0\\
&\hspace{17ex}\sin\phi=0
\end{align*}
より$\phi=0$となり、
\begin{align*}
\theta(0)=A\cos(\omega\cdot0+0)&=\theta_0\\
A\cos0&=\theta_0\\
A&=\theta_0
\end{align*}
従って
\begin{align*}
\theta(t)&=\theta_0\cos\omega t\\
\frac{\diff\theta}{\diff t}&=-\theta_0\omega\sin\omega t
\end{align*}
と表される。
ここで(1)の運動方程式に代入すると

\begin{align*}
ml\left(\frac{\diff\theta}{\diff t}\right)^2 & =S-mg\cos\theta \\
S &= mg\cos\theta + ml \left(\frac{\diff\theta}{\diff t}\right)^2 \\
&= mg\cos\theta + ml \left(- \theta_0 \omega \sin \omega t\right)^2 \\
&= mg\cos\theta + ml \theta_0^2 \omega^2 \sin ^2 \omega t \\
&= mg\cos\theta + ml \theta_0^2 \frac{g}{l} \sin ^2 \omega t \\
&= mg\cos\theta + mg\ \theta_0^2 \sin ^2 \omega t
\end{align*}

となる。$\theta , \theta_0$も十分に小さいので

\begin{align*}
\cos \theta \simeq 1, \qquad \theta_0^2 \sin ^2 \omega t \simeq 0
\end{align*}

と近似することができる。
従って、張力$S$は

\begin{align*}
S &= mg \cos \theta + mg\ \theta_0^2 \sin ^2 \omega t \\
& \simeq mg
\end{align*}

となる。