問題
単振動の変位 $y(t)$ が
\begin{eqnarray*}
y(t) = A \sin (\omega t)
\end{eqnarray*}
と表されているとき以下の問に答えよ。
(1) 速度 $v$ と変位 $y$ の関係を表わせ。
(2) 加速度 $a$ と変位 $y$ の関係を表わせ。
(3) 単振動は運動方程式 $\ddot{y}+\omega ^2 y =0$ を満たすことを示せ。
解答
(1)
速度$v$は
\begin{eqnarray*}
v = \frac{\diff y}{\diff t} &=& \frac{\diff}{\diff t} [A \sin (\omega t)] \\
\\
&=& A \omega \cos \omega t
\end{eqnarray*}
となる。
ここで、$\sin ^2 \omega t + \cos ^2 \omega t =1$の関係式より
\begin{eqnarray*}
\sin \omega t = \frac{y}{A} &, &\quad \cos \omega t = \frac{v}{A \omega} \\
\\
\sin ^2 \omega t + \cos ^2 \omega t &=& 1 \\
\\
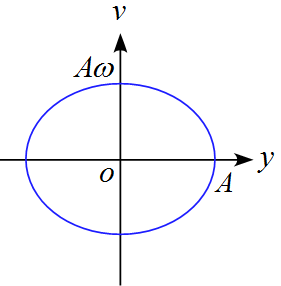
\left( \frac{y}{A} \right)^2 + \left( \frac{v}{A \omega} \right)^2 &=& 1 \\
\\
\frac{y^2}{A^2} + \frac{v^2}{A^2 \omega ^2} &=& 1
\end{eqnarray*}
となる。
(2)
加速度$a$は
\begin{eqnarray*}
a = \frac{\diff v}{\diff t} &=& \frac{\diff}{\diff t} [A \omega \cos \omega t] \\
\\
&=& -A \omega ^2 \sin \omega t \\
\\
&=& - \omega ^2 y
\end{eqnarray*}
となる。
(3)
(2)より、
\begin{eqnarray*}
a = \frac{\diff v}{\diff t} = \frac{\diff }{\diff t} \left( \frac{\diff y}{\diff t} \right) = \frac{\diff^2 y}{\diff t^2} = - \omega ^2 y
\end{eqnarray*}
であるから、
\begin{eqnarray*}
\ddot{y} &=& - \omega ^2 y \\
\\
\ddot{y} + \omega ^2 y &=& 0
\end{eqnarray*}
となる。