問題
滑らかな水平面上に2つの物体$\mathrm{A}$,$\mathrm{B}$が接触して置かれている。
力$F$を$\mathrm{A}$の側から水平に加えたとする。
2つの物体の質量をそれぞれ$m_\mathrm{A}$,$m_\mathrm{B}$として以下の問いに答えよ。
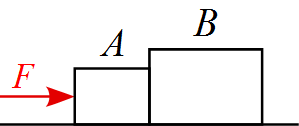
(1) 物体$\mathrm{A}$,$\mathrm{B}$の加速度$a$を求めよ。
(2) 物体$\mathrm{B}$に加わる力$f$を求めよ。
解答
右側を正に取り、作用する力を書き込むと、
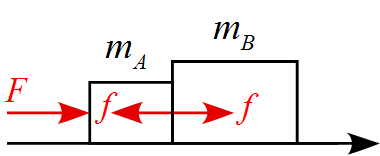
となる。
(1) 運動方程式はそれぞれ
\begin{align*}
\begin{cases}
m_\mathrm{A}a=F-f\\
m_\mathrm{B}a=f
\end{cases}
\end{align*}
となる。
2式の和をとると、
\begin{align*}
(m_\mathrm{A}+m_\mathrm{B})a=F-f+f\\
a=\frac{F}{m_\mathrm{A}+m_\mathrm{B}}
\end{align*}
となる。
(2) 運動方程式より
\begin{align*}
m_\mathrm{B}a&=f\\
m_\mathrm{B}\frac{F}{m_\mathrm{A}+m_\mathrm{B}}&=f\\
f&=\frac{m_\mathrm{B}}{m_\mathrm{A}+m_\mathrm{B}}F
\end{align*}
となる。