問題
天井に固定された滑車に2つの物体がひもでつながれて運動している。
物体の質量をそれぞれ$m_1$,$m_2$とする。($m_1 < m_2$)
滑車には摩擦がなく、ひもの質量は無視できるとし、
運動中はひもがたるまないとする。
以下の問いに答えよ。
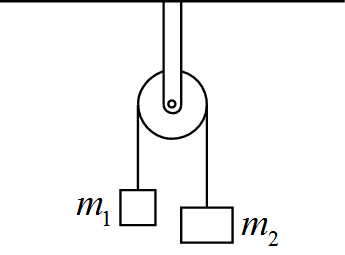
(1) それぞれの物体の運動方程式を記述せよ。
(2) 物体の加速度$a$を求めよ。
(3) ひもの張力$T$を求めよ。
解答
$m_1 < m_2$より、$m_1$は上昇し、$m_2$は下降すると考えられる。
従って下図のように軸をそれぞれ取り、作用する力を書き込むと、
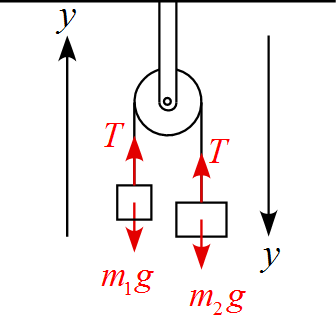
となる。
(1) 運動方程式は
\begin{align*}
\begin{cases}
m_1a=T-m_1g\\
m_2a=m_2g-T
\end{cases}
\end{align*}
となる。
(2) 2つの運動方程式を加えて整理すると、
\begin{align*}
m_1+m_2&=T-m_1g+m_2g-T\\
(m_1+m_2)a&=(m_2-m_1)g\\
a&=\frac{m_2-m_1}{m_2+m_1}g
\end{align*}
となる。
(3) 張力$T$は、
\begin{align*}
m_1=T-m_1g
\end{align*}
より、
\begin{align*}
T&=m_1a+m_1g\\
&=m_1\frac{m_2-m_1}{m_2+m_1}g+m_1g\\
&=m_1g\left(\frac{m_2-m_1}{m_2+m_1}+1\right)\\
&=m_1g\left(\frac{m_2-m_1+m_2+m_1}{m_1+m_2}\right)\\
&=m_1g\frac{2m_2}{m_1+m_2}\\
&=\frac{2m_1m_2}{m_1+m_2}g
\end{align*}
となる。
注) $\ m_1>m_2$の場合、加速度$a$は
\begin{align*}
a=\frac{m_2-m_1}{m_2+m_1}g<0
\end{align*}
となるので、設定した軸とは逆向きに運動することになります。