摩擦力のある物体の運動

問題

粗い水平面上に置かれた質量$m$の物体がある。
この物体に初速度$v_0$を与えて動かしたら距離$L$だけ移動して静止した。
動摩擦係数を$\mu’$としたとき移動距離$L$を求めよ。

解答

$x$軸、$y$軸を設定し、物体に作用する力を書き込むと、

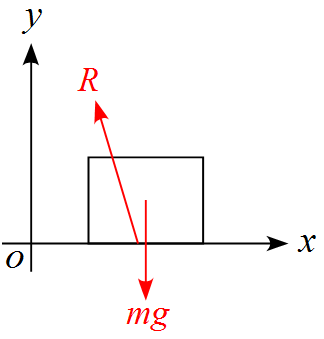
物体が運動している間に作用する力は、重力$mg$、抗力$R$の
2つとなります。

$x, y$軸に合わせて力を分解すると

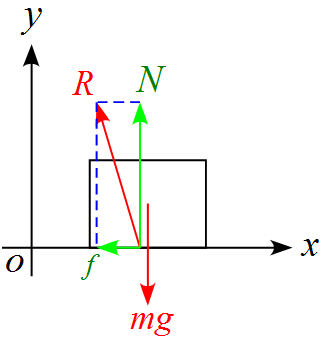
となります。

従って、運動方程式は
\begin{align*}
\begin{cases}
ma_x=-f\\
ma_y=N-mg
\end{cases}
\end{align*}
と表すことができる。
$a_y=0$より
\begin{align*}
0&=N-mg\\
N&=mg
\end{align*}
となる。
よって
\begin{align*}
ma_x=-f=-\mu’mg
\end{align*}
である。
よって
\begin{align*}
m\frac{\diff v_x}{\diff t}=-\mu’mg
\end{align*}
より
\begin{align*}
\frac{\diff v_x}{\diff t}&=-\mu’g\\
v_x&=-\mu’gt+C_1
\end{align*}
$t=0$で$v_x=v_0$なので
\begin{align*}
v_x(0)=-\mu’g\cdot 0+C_1&=v_0\\
C_1&=v_0
\end{align*}
よって
\begin{align*}
v_x(t)=-\mu’gt+v_0
\end{align*}
変位$x$は
\begin{align*}
v_x=\frac{\diff x}{\diff t}&=-\mu’g+v_0\\
x&=-\mu’gt^2\cdot \frac{1}{2}+v_0t+C_2
\end{align*}
$t=0$で$x=0$とすると
\begin{align*}
x(0)=-\frac{1}{2}\mu’g\cdot 0^2+v_0\cdot 0+C_2&=0\\
C_2&=0
\end{align*}
よって
\begin{align*}
x(t)=-\frac{1}{2}\mu’gt^2+v_0t
\end{align*}
となる。

物体が静止した時間を$t_1$とすると
\begin{align*}
v_x(t_1)=-\mu’gt_1+v_0&=0\\
\mu’gt_1&=v_0\\
\\
t_1&=\frac{v_0}{\mu’g}
\end{align*}
よって移動距離$L$は
\begin{align*}
L=x(t_1)=-\frac{1}{2}\mu’gt_1^2+v_0t_1&=-\frac{1}{2}\mu’g\left(\frac{v_0}{\mu’g}\right)^2+v_0\left(\frac{v_0}{\mu’g}\right)\\
\\
&=-\frac{v_0^2}{2\mu’g}+\frac{v_0^2}{\mu’g}\\
\\
&=\frac{v_0^2}{2\mu’g}
\end{align*}
となる。

別解
運動方程式は
\begin{align*}
m\frac{\diff v_x}{\diff t}=-\mu’mg
\end{align*}
の両辺に$v_x=\frac{\diff x}{\diff t}$をかけると
\begin{align*}
m\frac{\diff v_x}{\diff t}\cdot v_x &=-\mu’mg\cdot\frac{\diff x}{\diff t}\\
\frac{\diff}{\diff t}\Big(\frac{1}{2}mv_x^2\Big) &=\frac{\diff}{\diff t}\Big(-\mu’mgx\Big)
\end{align*}
となる。
\begin{align*}
\begin{cases}
t=0でx=0, v_x=v_0\\
t=t_1でx=L, v_x=0
\end{cases}
\end{align*}
の条件で$t$で積分すると、
\begin{align*}
\int_{v_0}^{0}\frac{\diff}{\diff t}\Big(\frac{1}{2}mv_x^2\Big)\diff t&=\int_{0}^{L}\frac{\diff}{\diff t}\Big(-\mu’mgx\Big)\diff t\\
\frac{1}{2}m\cdot 0^2-\frac{1}{2}mv_0^2&=-\mu’mg\cdot L-(-\mu’mg\cdot 0)\\
-\frac{1}{2}mv_0^2&=-\mu’mgL
\end{align*}
よって
\begin{align*}
L=\frac{v_0^2}{2\mu’g}
\end{align*}
となる。
これは物体の運動エネルギーが全て摩擦力による仕事に
変化したことを表している。