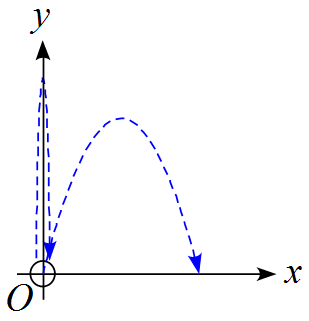
問題
質量$m$の質点が初速度$v_0$で投げ出される運動を考える。
鉛直方向に投げた場合の最高点と、斜方に投げ出された場合の水平到達距離が
等しくなるための方向を求めよ。
解答
2つの運動の組み合わせの問題である。
それぞれの運動について考えればよい。
まずは鉛直投げ上げにおいて作図し、作用する力を書き込むと
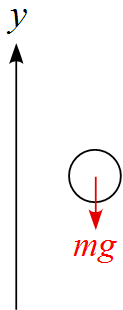
作用する力は重力$mg$のみである。
従って、運動方程式は
\begin{align*}
ma_y&=-mg\\
m\frac{\diff v_y}{\diff t}&=-mg
\end{align*}
となる。
速度$v_y$は
\begin{align*}
\frac{\diff v_y}{\diff t}&=-g\\
v_y&=-gt+C_1
\end{align*}
となる。$t=0$で$v_y=v_0$なので、
\begin{align*}
v_y(0)=-g\cdot 0+C_1&=v_0\\
C_1&=v_0
\end{align*}
よって
\begin{align*}
v_y(t)=-gt+v_0
\end{align*}
となる。
変位$y$は
\begin{align*}
v_y(t)=\frac{\diff y}{\diff t}&=-gt+v_0\\
y&=-gt^2\cdot\frac{1}{2}+v_0t+C_2
\end{align*}
となる。$t=0$で$y=0$なので
\begin{align*}
y(0)=-\frac{1}{2}g\cdot 0^2+v_0\cdot 0+C_2&=0\\
C_2&=0
\end{align*}
よって
\begin{align*}
y(t)=-\frac{1}{2}gt^2+v_0t
\end{align*}
となる。
最高点となる時間を$t_1$とすると、
\begin{align*}
v_y(t_1)=-gt_1+v_0&=0\\
t_1&=\frac{v_0}{g}
\end{align*}
である。
よって最高点$y(t_1)$は
\begin{align*}
y(t_1)=-\frac{1}{2}gt_1+v_0 t_1&=-\frac{1}{2}g\left(\frac{v_0}{g}\right)^2+v_0\frac{v_0}{g}\\
\\
&=-\frac{v_0^2}{2g}+\frac{v_0^2}{g}\\
\\
&=\frac{v_0^2}{2g}
\end{align*}
となる。
一方、斜方投射について作図をし、作用する力を書き込むと、
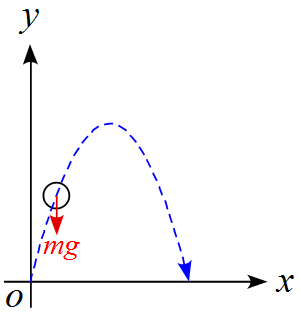
作用する力は重力$mg$のみである。
従って、運動方程式は
\begin{align*}
\begin{cases}
ma_x=0\\
ma_y=-mg
\end{cases}
\end{align*}
となる。
初期条件において、初速度は$v_0$であるので
$x$軸、$y$軸に分解すると
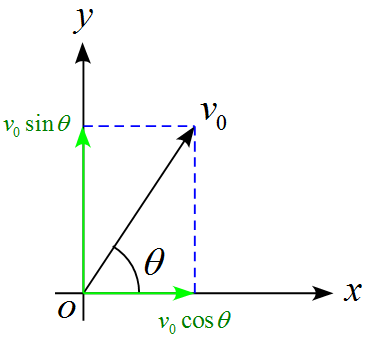
となる。
運動方程式より速度$v_x$は
\begin{align*}
a_x=\frac{\diff v_x}{\diff t}&=0\\
v_x&=C_3
\end{align*}
となる。$t=0$で$v_x=v_0\cos\theta$なので
\begin{align*}
v_x(0)=C_3=v_0\cos\theta
\end{align*}
より
\begin{align*}
v_x(t)=v_0\cos\theta
\end{align*}
となる。
変位$x$は
\begin{align*}
v_x=\frac{\diff x}{\diff t}&=v_0\cos\theta\\
x&=v_0\cos\theta\cdot t+C_4
\end{align*}
となる。$t=0$で$x=0$なので
\begin{align*}
x(0)=v_0\cos\theta\cdot 0+C_4&=0\\
C_4&=0
\end{align*}
よって
\begin{align*}
x(t)=v_0\cos\theta\cdot t
\end{align*}
となる。
また、速度$v_y$は
\begin{align*}
a_y=\frac{\diff v_y}{\diff t}&=-g\\
v_y&=-gt+C_5
\end{align*}
となる。$t=0$で$v_y=v_0\sin\theta$なので
\begin{align*}
v_y(0)=-g\cdot 0+C_5&=v_0\sin\theta\\
C_5&=v_0\sin\theta
\end{align*}
よって
\begin{align*}
v_y(t)=-gt+v_0\sin\theta
\end{align*}
となる。

作用する力は重力$mg$のみである。
従って、運動方程式は
\begin{align*}
\begin{cases}
ma_x=0\\
ma_y=-mg
\end{cases}
\end{align*}
となる。
初期条件において、初速度は$v_0$であるので
$x$軸、$y$軸に分解すると

となる。
運動方程式より速度$v_x$は
\begin{align*}
a_x=\frac{\diff v_x}{\diff t}&=0\\
v_x&=C_3
\end{align*}
となる。$t=0$で$v_x=v_0\cos\theta$なので
\begin{align*}
v_x(0)=C_3=v_0\cos\theta
\end{align*}
より
\begin{align*}
v_x(t)=v_0\cos\theta
\end{align*}
となる。
変位$x$は
\begin{align*}
v_x=\frac{\diff x}{\diff t}&=v_0\cos\theta\\
x&=v_0\cos\theta\cdot t+C_4
\end{align*}
となる。$t=0$で$x=0$なので
\begin{align*}
x(0)=v_0\cos\theta\cdot 0+C_4&=0\\
C_4&=0
\end{align*}
よって
\begin{align*}
x(t)=v_0\cos\theta\cdot t
\end{align*}
となる。
また、速度$v_y$は
\begin{align*}
a_y=\frac{\diff v_y}{\diff t}&=-g\\
v_y&=-gt+C_5
\end{align*}
となる。$t=0$で$v_y=v_0\sin\theta$なので
\begin{align*}
v_y(0)=-g\cdot 0+C_5&=v_0\sin\theta\\
C_5&=v_0\sin\theta
\end{align*}
よって
\begin{align*}
v_y(t)=-gt+v_0\sin\theta
\end{align*}
となる。