斜面の摩擦角

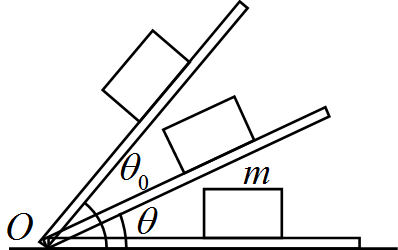
問題

水平面上に置かれた粗い板があり、質量$m$の物体が置かれている。
この板を左端$O$を支点として斜面の角度を変化させたとする。
静止摩擦係数を$\mu$としたとき、摩擦角$\theta_0$を表せ。

解答

斜面に平行な軸を$x$、斜面に垂直な軸を$y$とし、
物体に作用する力を書き込むと、

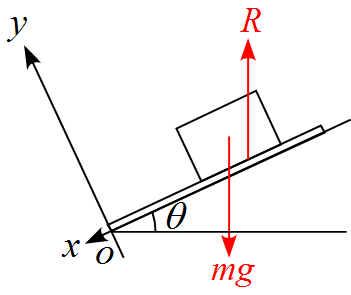
物体に作用する力は重力$mg$、抗力$R$となる。
$x$軸、$y$軸に合わせて力を分解すると、

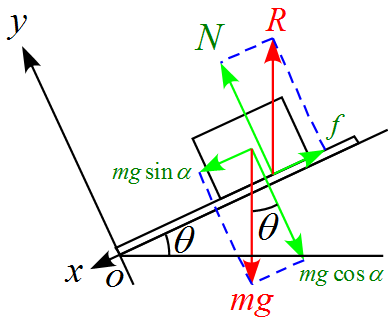
運動方程式は
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-f\\
ma_y=N-mg\cos\theta
\end{cases}
\end{align*}
と表すことができる。

$a_y=0, f=\mu N$より
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-\mu N\\
0=N-mg\cos\theta
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-\mu N\\
N=mg\cos\theta
\end{cases}
\end{align*}
となり、
\begin{align*}
ma_x=mg\sin\theta-\mu mg\cos\theta
\end{align*}
となる。

ここで、物体が$x$軸方向に動くためには
\begin{align*}
ma_x=mg\sin\theta-\mu mg\cos\theta>0
\end{align*}
が必要で、その限界の角度を$\theta_0$とすると、
\begin{align*}
mg\sin\theta_0-\mu mg\cos\theta_0&=0\\
\sin\theta_0&=\mu\cos\theta_0\\
\tan\theta_0&=\mu
\end{align*}
となる。
注）
厳密に言うと上式の運動方程式において摩擦係数は
動き始めた瞬間に動摩擦係数と変化することになる。