単振動のエネルギー

問題

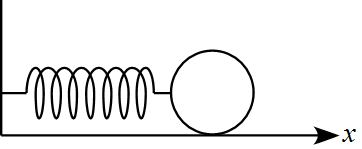
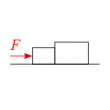
滑らかな水平面上にばねと物体が図のように設置されている。
物体の質量を$m$、ばね定数を$k$とする。
この物体が単振動する時、エネルギー保存則が成立することを運動方程式から導け。

解答

物体に作用する力は

ばねの復元力の大きさ$kx$のみである。
従って運動方程式は
\begin{align*}
m\frac{\diff v}{\diff t}=-kx
\end{align*}
となる。
両辺を$x$で積分すると
\begin{align*}
\int m\frac{\diff v}{\diff t}\diff x&=-\int kx\diff x\\
\int m\frac{\diff v}{\diff t}v\diff t&=-\int kx\diff x\\
\int\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2\right)\diff t&=-\int kx\diff x\\
\int\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2\right)\diff t+\int kx\diff x&=0\\
\frac{1}{2}mv^2+\frac{1}{2}kx^2&=C \qquad（C：\mbox{ 積分定数})
\end{align*}
よって運動エネルギーとばねによる弾性エネルギーの和が
常に時間に依らず一定であることを示している。
従って、力学的エネルギーの保存が成立している。