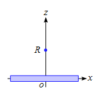
2球の正面衝突
問題
2球の正面衝突を考える。
この衝突において運動量が保持することを運動方程式を用いて示せ。
解答
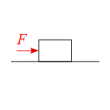
2球が衝突した瞬間は逆向きの同じ大きさの力が働くので
図に表すと
となる。
従って、A,Bそれぞれの運動方程式は
\begin{align*}
\begin{cases}
\dfrac{\diff p_\mathrm{A}}{\diff t}&=-F\\[2ex]
\dfrac{\diff p_\mathrm{B}}{\diff t}&=F
\end{cases}
\end{align*}
と表すことができる。
2つの式の和をとると、
\begin{align*}
\frac{\diff p_\mathrm{A}}{\diff t}+\frac{\diff p_\mathrm{B}}{\diff t}&=-F+F\\
\frac{\diff}{\diff t}\Big(p_\mathrm{A}+p_\mathrm{B}\Big)&=0
\end{align*}
よって運動量が時間的に変化しないので運動量は保存している。
ad
関連記事
-
-
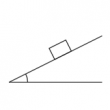
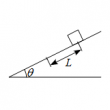
斜面を滑り下りる運動
問題 水平面をなす角$\theta$の粗い斜面上の点$\mathrm{A}$から物体を初速$v
-
-
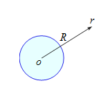
一様に帯電した球が作る電場
問題 一様な電荷密度$\rho$で帯電した半径$R$の球がある。以下の問いに答えよ。
-
-
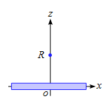
無限に長い直線に分布する電荷が作る電場
問題 単位長さあたりの電気量(線密度)が$\rho$である無限に長い直線上に電荷が分布している
-
-
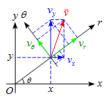
射法投射と鉛直投げ上げ
問題 質量$m$の質点が初速度$v_0$で投げ出される運動を考える。 鉛直方向に投げた場合の
-
-
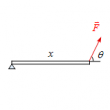
力のモーメントの計算
問題 以下の図に力$\vec{F}$が作用した場合の力のモーメント$\vec{M}$を計算
-
-
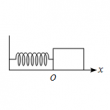
単振動の変位、速度、加速度
問題 なめらかな水平面上に壁からばねが取り付けれられている。 ばねは自然長の状態で静止してい
ad
- PREV
- 物体の質量が変化する運動
- NEXT
- 斜衝突の運動