問題
質量$m$の物体を自由落下させる。
以下の問いに答えよ。
但し、重力加速度は$g$とする。
(1) この運動の運動方程式を記述せよ。
(2) この運動において力学的エネルギーが保存していることを運動方程式から導け。
解答
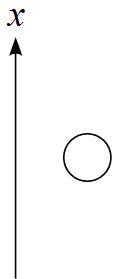
まずは作図をする。
上向きを正に軸を取ると
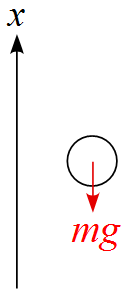
物体に作用する力を書き込むと
(1) 運動方程式は
\begin{align*}
ma&=-mg\\
m\frac{\diff v}{\diff t}&=-mg
\end{align*}
となる。
(2) 運動方程式の両辺を$x$で積分すると
\begin{align*}
m\frac{\diff v}{\diff t}&=-mg\\
\int m\frac{\diff v}{\diff t}\diff x&=-\int mg\diff x
\end{align*}
$\displaystyle v=\frac{\diff x}{\diff t}$より$\diff x=v\diff v$と表せるので
\begin{align*}
\int m\frac{\diff v}{\diff t}v\diff t&=-\int mg\diff x\\
\frac{1}{2}mv^2+C_1&=-mgx+C_2 \qquad(C_1, C_2 \mbox{:積分定数)}\\
\frac{1}{2}mv^2+mgx&=C
\end{align*}
従って、運動エネルギーと位置エネルギーの和が時間によらず
一定であるので力学的エネルギーは保存している。