問題
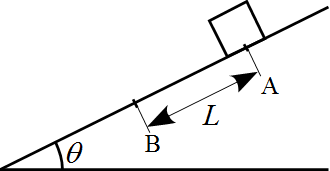
水平面をなす角$\theta$の粗い斜面上の点$\mathrm{A}$から物体を初速$v_0$で斜面に沿って下向きに
打ち出した。物体の質量を$m$、重力加速度を$g$、動摩擦係数を$\mu_k$とする。
点$\mathrm{A}$から距離$L$だけ進んだ点$\mathrm{B}$において以下の問いに答えよ。
(1) 重力がした仕事を求めよ。
(2) 垂直抗力がした仕事を求めよ。
(3) 動摩擦力がした仕事を求めよ。
(4) 点$\mathrm{B}$における速度$v_1$を求めよ。
解答
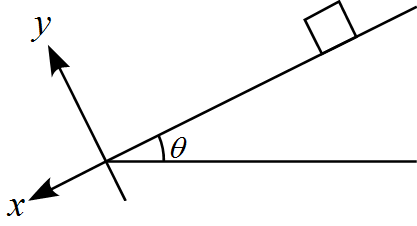
この運動では2次元的に運動するので2つの軸を設定する。
斜面に平行な軸を$x$とし、斜面に垂直な軸を$y$とする。
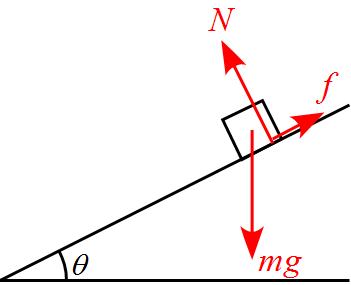
物体に作用する力を書き込むと、
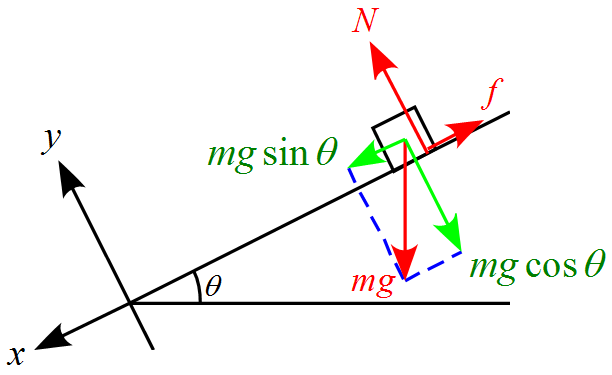
$x$軸、$y$軸に合わせて力を分解すると、
となる。
運動方程式は、それぞれの加速度$a_x$, $a_y$として、
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-f \\
ma_y=N-mg\cos\theta
\end{cases}
\end{align*}
と表すことができる。
$a_y=0$, $f=\mu_k N$より
\begin{align*}
\begin{cases}
ma_x &=& mg\sin\theta-\mu_kN\\
0 &=& N-mg\cos\theta
\end{cases}
\end{align*}
となる。
両辺に$v_x = \frac{\diff x}{\diff t}$をかけると
\begin{align*}
m\frac{\diff v_x}{\diff t}v_x&=\Big(mg\sin\theta-\mu_kmg\cos\theta\Big)\frac{\diff x}{\diff t}\\
\frac{\diff}{\diff t}\left(\frac{1}{2}mv_x^2\right)&=\frac{\diff}{\diff t}\Big(mg\sin\theta\cdot x-\mu_kmg\cos\theta\cdot x\Big)
\end{align*}
両辺を$t$で積分すると
\begin{align*}
\int_{v_0}^{v_1}\frac{\diff}{\diff t}\left(\frac{1}{2}mv_x^2\right)\diff t&=\int_{0}^{L}\frac{\diff}{\diff t}\Big(mg\sin\theta\cdot x-\mu_kmg\cos\theta\cdot x\Big)\diff t\\
\left[\frac{1}{2}mv_x^2\right]_{v_0}^{v_1}&=\Big[mg\sin\theta\cdot x-\mu_kmg\cos\theta\cdot x\Big]_0^L\\
\frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2&=mg\sin\theta\cdot L-\mu mg\cos\theta\cdot L
\end{align*}
となる。
ここで、右辺の第1項は重力による仕事、第2項は動摩擦力がする仕事である。
垂直抗力は進行方向と垂直なので仕事はしない。
従って、
(1) $mg\sin\theta\cdot L$
(2) $0$
(3) $-\mu_kmg\cos\theta\cdot L$
となる。
(4) さらに
\begin{align*}
\frac{1}{2}mv_1^2&=\frac{1}{2}mv_0^2+mg\sin\theta\cdot L-\mu_kmg\cos\theta\cdot L\\
v_1^2&=\frac{2}{m}\left(\frac{1}{2}mv_0^2+mg\sin\theta\cdot L-\mu_kmg\cos\theta\cdot L\right)\\
&=v_0^2+2g(\sin\theta-\mu_k\cos\theta)L\\
\\
v_1&=\sqrt{v_0^2+2g(\sin\theta-\mu_k\cos\theta)L}
\end{align*}
となる。