摩擦係数の定義

問題

水平面上に質量$m$の物体が置かれている。
水平方向から力$F$を加えて動かそうとしたところ
力が$f_0$を超えたときに動き出した。

(1) 面と物体の間の静止摩擦係数$\mu_0$を求めよ。

(2) 力$F$と摩擦係数$\mu$の関係をグラフで表せ。

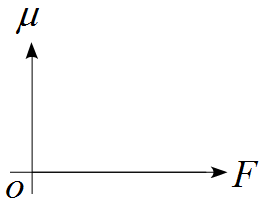
解答

$x$軸,$y$軸を設定し、作用する力を書き込むと、

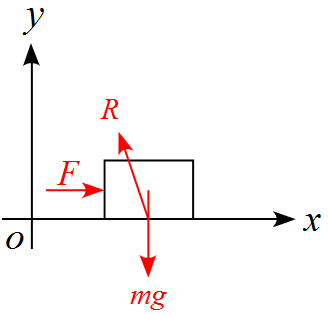
物体に作用する力は、重力$mg$、抗力$R$、加えた力$F$の3つとなる。
$x$軸、$y$軸に合わせて力を分解すると、

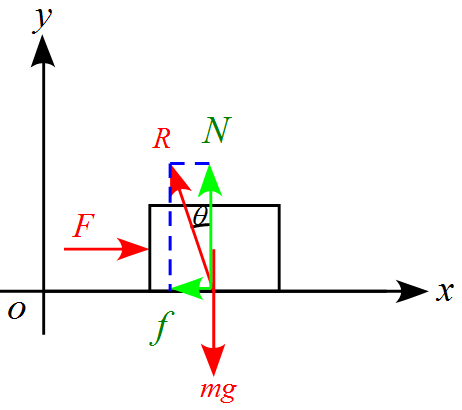
となる。
従って、運動方程式は

$$\begin{align*} \begin{cases} ma_x=F-f\\ ma_y=N-mg \end{cases} \end{align*}$$
と表すことができる。
$a_y=0$より
$$\begin{align*} 0&=N-mg\\ N&=mg \end{align*}$$
となる。
摩擦係数の定義は
$$\begin{align*} \mu=\frac{f}{N}=\tan\theta \end{align*}$$
である。
静止している間は$|F|=|f|$である。
$|F|=f_0$となったときの摩擦係数は
$$\begin{align*} \mu=\frac{f_0}{N}=\frac{f_0}{mg} \end{align*}$$
と表される。

(2) 力Fと摩擦係数$\mu$の関係は

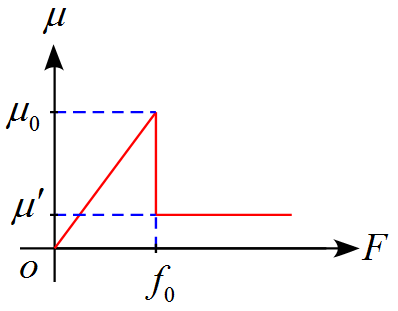
となる。