等速円運動の位置、速度、加速度

問題

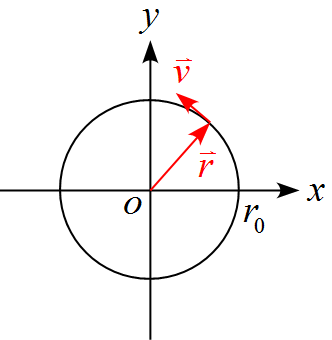
半径$r_0$、速さ$v_0$で等速円運動をしている物体について
以下の問いに答えよ。

(1) 速度ベクトル$\vec{v}$と位置ベクトル$\vec{r}$が直交していることを示せ。

(2) 速度ベクトル$\vec{v}$と加速度ベクトル$\vec{a}$が直交していることを示せ。

(3) 加速度の大きさ$|\vec{a}|$を求めよ。

解答

直交を示す方法として、$\vec{v}\cdot\vec{r}=0$を示す方法を用いる。
$\vec{r}$と$\vec{v}$のそれぞれをそれ自身と内積を取ると
等速円運動より
\begin{align*}
\vec{r}\cdot\vec{r}&=|\vec{r}||\vec{r}|\cos\theta\\
&=|\vec{r}|^2\cdot1 \qquad \mbox{($\theta=0$より)}\\
&=|\vec{r}|^2\\
&=r_0^2\\
\vec{v}\cdot\vec{v}&=|\vec{v}||\vec{v}|\cos\theta\\
&=|\vec{v}|^2\cdot1 \qquad \mbox{($\theta=0$より)}\\
&=|\vec{v}|^2\\
&=v_0^2
\end{align*}
となる。

(1)
$\vec{r}\cdot\vec{r}=r_0^2$の両辺を$t$で微分すると
\begin{align*}
\frac{\diff}{\diff t}(\vec{r}\cdot\vec{r})=\frac{\diff\vec{r}}{\diff t}\cdot\vec{r}+\vec{r}\cdot\frac{\diff\vec{r}}{\diff t}&=\frac{\diff}{\diff t}(r_0^2)\\
2\vec{r}\cdot\frac{\diff\vec{r}}{\diff t}&=0\\
\vec{r}\cdot\vec{v}&=0
\end{align*}
従って、$\vec{r}$と$\vec{v}$は直交している。

(2)
$\vec{v}\cdot\vec{v}=v_0^2$の両辺を$t$で微分すると
\begin{align*}
\frac{\diff}{\diff t}(\vec{v}\cdot\vec{v})=\frac{\diff\vec{v}}{\diff t}\cdot\vec{v}+\vec{v}\cdot\frac{\diff\vec{v}}{\diff t}&=\frac{\diff}{\diff t}(v_0^2)\\
2\vec{v}\cdot\frac{\diff\vec{v}}{\diff t}&=0\\
\vec{v}\cdot\vec{a}&=0
\end{align*}
従って、$\vec{r}$と$\vec{a}$は直交している。

(3)
$\vec{r}\cdot\vec{v}=0$の両辺を$t$で微分すると
\begin{align*}
\frac{\diff}{\diff t}(\vec{r}\cdot\vec{v})=\frac{\diff\vec{r}}{\diff t}\cdot\vec{v}+\vec{r}\cdot\frac{\diff\vec{v}}{\diff t}&=0\\
\vec{v}\cdot\vec{v}+\vec{r}\cdot\vec{a}&=0\\
v_0^2+\vec{r}\cdot\vec{a}&=0\\
\vec{r}\cdot\vec{a}&=-v_0^2\\
|\vec{r}||\vec{a}|\cos\theta&=-v_0^2\\
|\vec{r}||\vec{a}|\cdot -1&=-v_0^2\qquad \mbox{($\theta=\pi$より)} \\
|\vec{a}|&=\frac{v_0^2}{|\vec{r}|}\\
|\vec{a}|&=\frac{v_0^2}{r_0}
\end{align*}
となる。