球の変化率を考える
問題
風船に空気を入れ、膨らませる場合の変化について考える。
風船に毎秒$v_0$の割合で吹きこむとする。
$t=0$で半径$r$は$0$であるとし、スタートした瞬間から半径$r$の球となって
膨らむものとする。
半径の増加率$\dfrac{\diff r}{\diff t}$を求めよ。
解答
時刻$t$のとき$v_0t$の空気が入っているので、その半径を$r$とすると
\begin{align*}
\frac{4\pi}{3}r^3=v_0t
\end{align*}
である。
よって半径$r$について
\begin{align*}
r^3&=\frac{3}{4\pi}v_0t\\
&=\frac{3v_0}{4\pi}t\\
r&=\left(\frac{3v_0}{4\pi}\right)^{\frac{1}{3}}t^{\frac{1}{3}}
\end{align*}
となる。
よって$t$で微分をすると
\begin{align*}
\frac{\diff r}{\diff t}&=\frac{\diff}{\diff t}\left[\left(\frac{3v_0}{4\pi}\right)^{\frac{1}{3}}t^{\frac{1}{3}}\right]\\
&=\left(\frac{3v_0}{4\pi}\right)^{\frac{1}{3}}\cdot\frac{\diff}{\diff t}t^{\frac{1}{3}}\\
&=\left(\frac{3v_0}{4\pi}\right)^{\frac{1}{3}}\cdot\frac{1}{3}t^{-\frac{2}{3}}\\
&=\frac{1}{3}\left(\frac{3v_0}{4\pi}\right)^{\frac{1}{3}}t^{-\frac{2}{3}}
\end{align*}
となる。
$t=\dfrac{4}{3}\pi r^3\cdot\dfrac{1}{v_0}$を代入して$r$で表すと
\begin{align*}
\frac{\diff r}{\diff t}&=\frac{1}{3}\left(\frac{3v_0}{4\pi}\right)^{\frac{1}{3}}t^{-\frac{2}{3}}\\
&=\frac{1}{3}\left[\frac{3v_0}{4\pi}\left(\frac{3v_0}{4\pi r^3}\right)^2\right]^{\frac{1}{3}}\\
&=\frac{1}{3}\left(\frac{3^3v_0^3}{4^3\pi^3r^6}\right)^{\frac{1}{3}}\\
&=\frac{1}{3}\frac{3v_0}{4\pi r^2}\\
&=\frac{v_0}{4\pi r^2}
\end{align*}
となる。
ad
関連記事
-
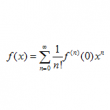
-
べき級数展開と近似式
問題 関数$f(x)=(1+x)^\alpha$($\alpha$は実数)について (1
-
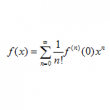
-
マクローリン展開の計算
問題 次の関数$f(x)$をマクローリン級数に展開せよ。 (1) $f(x)=\sin
-
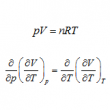
-
偏微分の状態方程式への利用
問題 理想気体の状態方程式は \begin{align*}
-
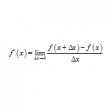
-
微分の定義から導関数を求める
問題 ある関数$f(x)$の導関数$f'(x)$は \begin{align*}
-
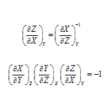
-
偏微分の関係式の導出
問題 以下の関係式を導出せよ。 (1) $\displaystyle \left( \f
ad
- PREV
- 等速円運動の加速度
- NEXT
- 円の面積変化を考える