ベクトルの外積

問題

3次元の直交座標系を考える。
ベクトルの成分を
\begin{align*}
\vec{A}=(A_x, A_y, A_z)\\
\vec{B}=(B_x, B_y, B_z)
\end{align*}
とする。

(1) この2つのベクトルの外積が

\begin{align*}
\vec{A}\times\vec{B}=\left(
\begin{array}{ccc}
A_yB_z-A_zB_y\\
A_zB_x-A_xB_z\\
A_xB_y-A_yB_x
\end{array}
\right)
\end{align*}
となることを示せ。

(2) 外積の大きさ$|\vec{A}\times\vec{B}|$が、$\vec{A}$と$\vec{B}$がつくる平行四辺形の面積に等しいことを示せ。

解答

(1) $x$軸、$y$軸、$z$軸方向の単位ベクトルをそれぞれ$\vec{i},\vec{j},\vec{k}$とすると、
\begin{align*}
\vec{A}=A_x\vec{i}+A_y\vec{j}+A_z\vec{k}\\
\vec{B}=B_x\vec{i}+B_y\vec{j}+B_z\vec{k}
\end{align*}
となる。
よってベクトルの外積は、
\begin{align*}
\vec{A}\times\vec{B}=&(A_x\vec{i}+A_y\vec{j}+A_z\vec{k})\times(B_x\vec{i}+B_y\vec{j}+B_z\vec{k})\\
=&A_x\vec{i}\times B_x\vec{i}+A_x\vec{i}\times B_y\vec{j}+A_x\vec{i}\times B_z\vec{k}+\\
&A_y\vec{j}\times B_x\vec{i}+A_y\vec{j}\times B_y\vec{j}+A_y\vec{j}\times B_z\vec{k}+\\
&A_z\vec{k}\times B_x\vec{i}+A_z\vec{k}\times B_y\vec{j}+A_z\vec{k}\times B_z\vec{k}
\end{align*}
ここで単位ベクトルに対して、
\begin{align*}
\vec{i}\times\vec{i}=\vec{j}\times\vec{j}=\vec{k}\times\vec{k}=0\\
\vec{i}\times\vec{j}=\vec{k},\ \vec{j}\times\vec{k}=\vec{i},\ \vec{k}\times\vec{i}=\vec{j}
\end{align*}
が成立する。
従って
\begin{align*}
\vec{A}\times\vec{B}=&A_xB_y\vec{i}\times\vec{j}+A_xB_z\vec{i}\times\vec{k}+\\
&A_yB_x\vec{j}\times\vec{i}+A_yB_z\vec{j}\times\vec{k}+\\
&A_zB_x\vec{k}\times\vec{i}+A_zB_y\vec{k}\times\vec{j}\\
=&A_xB_y\vec{k}+A_xB_z(-\vec{j})+A_yB_x(-\vec{k})+A_yB_z\vec{i}+A_zB_x\vec{j}+A_zB_y(-\vec{i})\\
=&(A_yB_z-A_zB_y)\vec{i}+(A_zB_x-A_xB_z)\vec{j}+(A_xB_y-A_yB_x)\vec{k}\\
=&\left(
\begin{array}{ccc}
A_yB_z-A_zB_y\\
A_zB_x-A_xB_z\\
A_xB_y-A_yB_x
\end{array}
\right)
\end{align*}
となる。

(2)
\begin{align*}
|\vec{A}\times\vec{B}|^2=&\left|\left(
\begin{array}{ccc}
A_yB_z-A_zB_y\\
A_zB_x-A_xB_z\\
A_xB_y-A_yB_x
\end{array}
\right)\right|^2\\
=&(A_yB_z-A_zB_y)^2+(A_zB_x-A_xB_z)^2+(A_xB_y-A_yB_x)^2\\
=&A_y^2B_z^2+A_z^2B_y^2-2A_yB_zA_zB_y+\\
&A_z^2B_x^2+A_x^2B_z^2-2A_zB_xA_xB_z+\\
&A_x^2B_y^2+A_y^2B_x^2-2A_xB_yA_yB_x\\
=&A_x^2(B_y^2+B_z^2)+A_y^2(B_x^2+B_z^2)+A_z^2(B_x^2+B_y^2)\\
&-2(A_xB_yA_yB_x+A_xB_zA_zB_x+A_yB_zA_zB_y)\\
=&A_x^2(B_x^2+B_y^2+B_z^2)+A_y^2(B_x^2+B_y^2+B_z^2)+A_z^2(B_x^2+B_y^2+B_z^2)\\
&-(A_x^2B_x^2+A_y^2B_y^2+A_z^2B_z^2)-2(A_xB_yA_yB_x+A_xB_zA_zB_x+A_yB_zA_zB_y)\\
=&(A_x^2+A_y^2+A_z^2)(B_x^2+B_y^2+B_z^2)-\{(A_xB_x)^2+(A_yB_y)^2+(A_zB_z)^2\\
&+2(A_xB_x)(A_yB_y)+2(A_xB_x)(A_zB_z)+2(A_yB_y)(A_zB_z)\}\\
=&(A_x^2+A_y^2+A_z^2)(B_x^2+B_y^2+B_z^2)-(A_xB_x+A_yB_y+A_zB_z)^2\\
=&|\vec{A}|^2|\vec{B}|^2-(\vec{A}\cdot\vec{B})^2\\
=&|\vec{A}|^2|\vec{B}|^2-(|\vec{A}||\vec{B}|\cos\theta)^2\\
=&|\vec{A}|^2|\vec{B}|^2-|\vec{A}|^2|\vec{B}|^2\cos^2\theta\\
=&|\vec{A}|^2|\vec{B}|^2(1-\cos^2\theta)\\
=&|\vec{A}|^2|\vec{B}|^2\sin^2\theta
\end{align*}
よって
\begin{align*}
|\vec{A}\times\vec{B}|=|\vec{A}||\vec{B}|\sin\theta
\end{align*}
となる。一方、$\vec{A}$と$\vec{B}$がつくる平行四辺形は

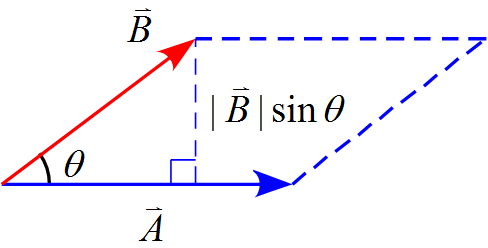
となるのでこの面積$S$は
\begin{align*}
S=|\vec{A}||\vec{B}|\sin\theta
\end{align*}
である。
従って、$|\vec{A}\times\vec{B}|$は$\vec{A}$と$\vec{B}$がつくる平行四辺形の面積に等しい。