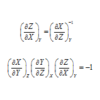マクローリン展開の計算
問題
次の関数$f(x)$をマクローリン級数に展開せよ。
(1) $f(x)=\sin x$
(2) $f(x)=\cos x$
(3) $f(x)=e^x$
解答
関数$f(x)$のマクローリン展開は
\begin{align*}
f(x)=\sum_{n=0}^{\infty}\frac{1}{n!}f^{(n)}(0)x^n
\end{align*}
で与えられる。
(1) \begin{align*}
f(0)&=\sin0=0\\
f'(0)&=\cos0=1\\
f”(0)&=-\sin0=0\\
f”'(0)&=-\cos0=-1
\end{align*}
よって
\begin{align*}
f(x)=\sin x&=0+\frac{1}{1!}x+\frac{0}{2!}x^2+\frac{-1}{3!}x^3+\frac{0}{4!}x^4+\frac{1}{5!}x^5\cdots\\
&=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+\frac{(-1)^n}{(2n+1)!}x^{2n+1}+\cdots
\end{align*}
となる。
(2) \begin{align*}
f(0)&=\cos0=1\\
f'(0)&=-\sin0=0\\
f”(0)&=-\cos0=-1\\
f”'(0)&=\sin0=0
\end{align*}
よって
\begin{align*}
f(x)=\cos x&=1+\frac{0}{1!}x+\frac{-1}{2!}x^2+\frac{0}{3!}x^3+\frac{1}{4!}x^4+\frac{0}{5!}x^5\cdots\\
&=1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+\frac{(-1)^n}{(2n)!}x^{2n}+\cdots
\end{align*}
となる。
(3) \begin{align*}
f(0)&=e^0=1\\
f'(0)&=e^0=1\\
f”(0)&=e^0=1
\end{align*}
よって
\begin{align*}
f(x)=e^x&=1+\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots\\
&=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!}+\cdots
\end{align*}
となる。
ad
関連記事
-
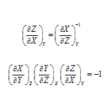
-
偏微分の関係式の導出
問題 以下の関係式を導出せよ。 (1) $\displaystyle \left( \f
-
-
単振動の変位と速度、加速度の関係
問題 単振動の変位 $y(t)$ が \begin{eqnarray*} y(t) =
-
-
無限に長い直線に分布する電荷が作る電場
問題 単位長さあたりの電気量(線密度)が$\rho$である無限に長い直線上に電荷が分布している
-
-
加速度から速度、変位を求める
問題 $x$軸を運動する質点の加速度が \begin{align*}
-
-
球の表面に一様に帯電した球が作る電場
問題 一様な面密度$\sigma$で球表面に帯電した半径$R$の球がある。以下の問いに答えよ。
-
-
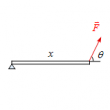
力のモーメントの計算
問題 以下の図に力$\vec{F}$が作用した場合の力のモーメント$\vec{M}$を計算
-
-
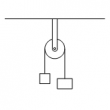
固定された滑車の運動
問題 天井に固定された滑車に2つの物体がひもでつながれて運動している。 物体の質量をそれぞれ
-
-
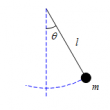
単振り子のエネルギー保存
問題 質量$m$の物体が長さ$l$の糸につるされている。 この物体の単振り子運動においてエネ
ad
- PREV
- 密度が一様でない棒の質量
- NEXT
- ベクトルの内積