問題
質点が原点を中心に半径$r$、角速度$\omega$の等速円運動を行っている。
この運動の加速度ベクトルは
\begin{align*}
\vec{a}=-\omega^2\vec r
\end{align*}
と表されることを示せ。
解答
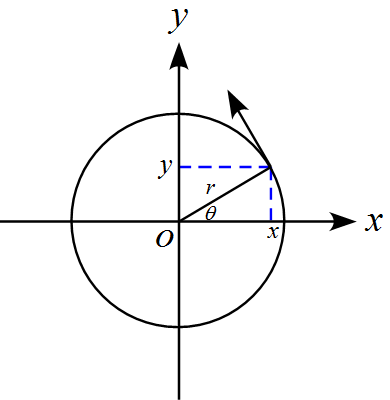
作図をすると
ある時刻$t$における角度を$\theta$とすると
\begin{align*}
\theta=\omega t+\alpha \qquad(\alpha \mbox{はある定数)}
\end{align*}
と表される。
位置$x$, $y$は
\begin{align*}
\begin{cases}
x=r\cos\theta&=r\cos(\omega t+\alpha)\\
y=r\sin\theta&=r\sin(\omega t+\alpha)
\end{cases}
\end{align*}
となる。
これを$t$で微分して$v_x$, $v_y$を求めると
\begin{align*}
v_x=\frac{\diff x}{\diff t}&=\frac{\diff}{\diff t}\Big[r\cos(\omega t+\alpha)\Big]\\
&=-r\omega\sin(\omega t+\alpha)\\
&=-r\omega y\\
&\\
v_y=\frac{\diff y}{\diff t}&=\frac{\diff}{\diff t}\Big[r\sin(\omega t+\alpha)\Big]\\
&=-r\omega\cos(\omega t+\alpha)\\
&=r\omega x
\end{align*}
となる。
さらに$t$で微分して$a_x$, $a_y$を求めると
\begin{align*}
a_x=\frac{\diff v_x}{\diff t}&=\frac{\diff}{\diff t}\Big[-r\omega\sin(\omega t+\alpha)\Big]\\
&=-r\omega^2\cos(\omega t+\alpha)\\
&=-\omega^2x\\
&\\
a_y=\frac{\diff v_y}{\diff t}&=\frac{\diff}{\diff t}\Big[-r\omega\cos(\omega t+\alpha)\Big]\\
&=-r\omega^2\sin(\omega t+\alpha)\\
&=-\omega^2y
\end{align*}
となる
よって加速度ベクトル$\vec a$は
\begin{align*}
\vec a=
\begin{pmatrix}
a_x\\
a_y
\end{pmatrix}
=
\begin{pmatrix}
-\omega^2x\\
-\omega^2y
\end{pmatrix}
&=-\omega^2
\begin{pmatrix}
x\\
y
\end{pmatrix}
\\
&=-\omega^2\vec r
\end{align*}
となる。