問題
ヤングの実験を考える。
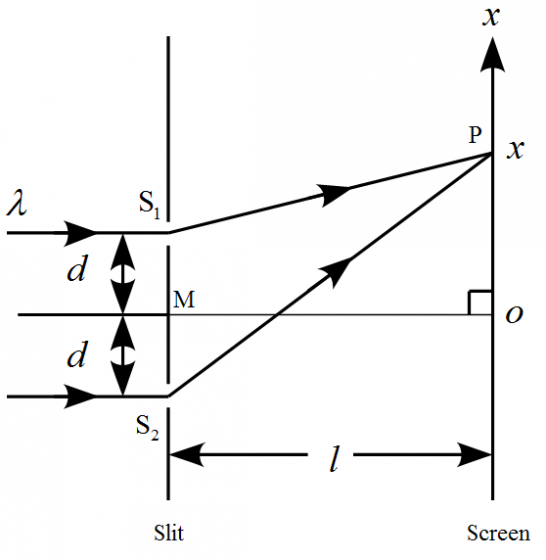
図のように、平行な2つの幅の狭いスリット$\mathrm{S}_1$, $\mathrm{S}_2$に垂直に光を当てると、
スリットに平行なスクリーン上に明暗の干渉縞が映し出される。
2つのスリットの間隔を$2d$、スクリーンとスリットの距離を$l$とする。
スリットの中点を$\mathrm{M}$、点$\mathrm{M}$からスクリーンへ垂線$\mathrm{M}\mathrm{O}$を引き、
スクリーン上の点$\mathrm{O}$を原点とする。
スクリーン上の位置$x$に点$\mathrm{P}$を取る。
スリットに当てる光の波長を$\lambda$として、スクリーン上の原点$\mathrm{O}$付近にできる
干渉縞の間隔を求めよ。
但し、$d\ll l$, $x\ll l$として近似式の1次まで考えるとする。
解答
光路差が光の波長の整数倍になるとき干渉して強め合う。
従って明線ができる条件は
\begin{align*}
\mbox{光路差}=\mathrm{S}_2\mathrm{P}-\mathrm{S}_1\mathrm{P}=m \lambda \qquad(m \mbox{は整数)}
\end{align*}
である。
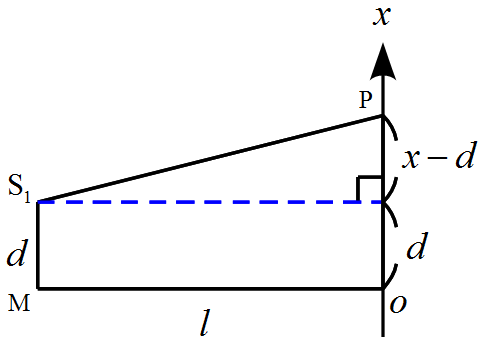
$\mathrm{S}_1\mathrm{P}$について
\begin{align*}
\mathrm{S}_1\mathrm{P}=\sqrt{l^2+(x-d)^2}&=\sqrt{l^2\left\{1+\frac{(x-d)^2}{l^2}\right\}}\\
&=l\sqrt{1+\left(\frac{x-d}{l}\right)^2}
\end{align*}
ここで、$d\ll l$, $x\ll l$より$\left(\dfrac{x-d}{l}\right)^2\ll l$である。
よって$(1+x)^\alpha\approx1+\alpha x$の近似を利用すると
\begin{align*}
\sqrt{1+\left(\frac{x-d}{l}\right)^2}&=\left\{1+\left(\frac{x-d}{l}\right)^2\right\}^\frac{1}{2}\\
&\approx1+\frac{1}{2}\left(\frac{x-d}{l}\right)^2
\end{align*}
となる。
よって
\begin{align*}
\mathrm{S}_1\mathrm{P}=l\sqrt{1+\left(\frac{x-d}{l}\right)^2}&\approx l\left\{1+\frac{1}{2}\left(\frac{x-d}{l}\right)^2\right\}\\
&=l+\frac{(x-d)^2}{2l}
\end{align*}
である。
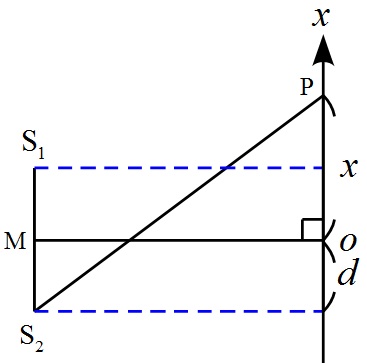
同様に$\mathrm{S}_2\mathrm{P}$について
\begin{align*}
\mathrm{S}_2\mathrm{\mathrm{P}}=\sqrt{l^2+(x+d)^2}&=\sqrt{l^2\left\{1+\frac{(x+d)^2}{l^2}\right\}}\\
&=l\sqrt{1+\left(\frac{x+d}{l}\right)^2}\\
&\approx l\left\{1+\frac{1}{2}\left(\frac{x+d}{l}\right)^2\right\}\\
&=l+\frac{(x+d)^2}{2l}
\end{align*}
となる。
よって光路差は
\begin{align*}
\mathrm{S}_2\mathrm{P}-\mathrm{S}_1\mathrm{P}&=l+\frac{(x+d)^2}{2l}-\left\{l+\frac{(x-d)^2}{2l}\right\}\\
&=l+\frac{x^2+2xd+d^2}{2l}-\left\{l+\frac{x^2-2xd+d^2}{2l}\right\}\\
&=\frac{4xd}{2l}\\
&=\frac{2dx}{l}
\end{align*}
となる。
よって$m$番目の強め合う条件は
\begin{align*}
\frac{2dx_m}{l}&=m\lambda\\
x_m&=m\frac{l\lambda}{2d}
\end{align*}
である。
従って干渉縞の間隔$\Delta x$は
\begin{align*}
\Delta x=x_{m+1}-x_m&=(m+1)\frac{l\lambda}{2d}-m\frac{l\lambda}{2d}\\
&=\frac{l\lambda}{2d}
\end{align*}
となる。