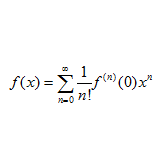等速円運動の加速度
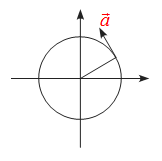
問題 質点が原点を中心に半径$r$、角速度$\omega$の等速円運動を行っている。 この運動の加速度ベクトルは \begin{align*} \vec{a}=-\omega^2\vec r \end{align*} と表されることを示せ。 解答 作図をすると ある時刻$t$における角度を$\theta$とすると \begin{align*} \theta=\omega t+\alpha \qquad(\alpha \mbox{はある定数)} \end{align*} と表される。 位置$x$, $y$は ...
ヤングの実験
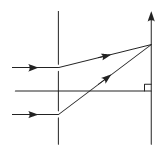
問題 ヤングの実験を考える。 図のように、平行な2つの幅の狭いスリット$\mathrm{S}_1$, $\mathrm{S}_2$に垂直に光を当てると、 スリットに平行なスクリーン上に明暗の干渉縞が映し出される。 2つのスリットの間隔を$2d$、スクリーンとスリットの距離を$l$とする。 スリットの中点を$\mathrm{M}$、点$\mathrm{M}$からスクリーンへ垂線$\mathrm{M}\mathrm{O}$を引き、 スクリーン上の点$\mathrm{O}$を原点とする。 スクリーン上の位置$x ...
微分方程式~自由落下
問題 質量$m$の物体を自由落下させることを考える。 鉛直下向きを正の向きにとり高さ$z$を測ると、物体の持つ全エネルギーは \begin{align*} E=\frac{1}{2}mv^2-mgz \end{align*} と書ける。 $t=0$で$z=0$にあり、全エネルギーが保存されることを用いて 高さ$z(t)$を求めよ。 但し、$v$は速度、$g$は重力加速度を表しているとする。 解答 全エネルギー$E$を変形すると \begin{align*} E&=\frac{1}{2}mv^2-mgz\\ ...
べき級数展開と近似式
問題 関数$f(x)=(1+x)^\alpha$($\alpha$は実数)について (1) べき級数展開を求めよ。 (2) $|x|\ll$のとき、$f(x)$の$x$に関する2次の項までの近似式を求めよ。 解答 (1) 関数$f(x)$のべき級数展開は \begin{align*} f(x)=\sum_{n=0}^\infty \frac{1}{n!}f^{(n)}(0)x^n \end{align*} で与えられる。 ここで \begin{align*} f(0)&=(1+0)^\alpha=1\\ ...
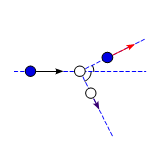
斜衝突の運動
問題 質量が等しい2つの質点A, Bがある。 静止しているBに速度$v_0$でAが衝突し、その後、図のようになす角$\alpha$, $\beta$で、 速度$v$, $V$でそれぞれ運動した。 この衝突は弾性衝突であり、衝突の前後で運動エネルギーは不変であるとする。 (1) 角$\alpha+\beta$を求めよ。 (2) 速度比$\dfrac{v}{V}$を$\beta$を用いて表せ。 解答 (1) 運動量保存則より \begin{align*} m\vec{v_0}=m\vec{v}+m\vec{V ...
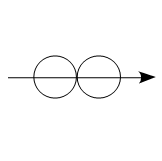
2球の正面衝突
問題 2球の正面衝突を考える。 この衝突において運動量が保持することを運動方程式を用いて示せ。 解答 2球が衝突した瞬間は逆向きの同じ大きさの力が働くので 図に表すと となる。 従って、A,Bそれぞれの運動方程式は \begin{align*} \begin{cases} \dfrac{\diff p_\mathrm{A}}{\diff t}&=-F\\[2ex] \dfrac{\diff p_\mathrm{B}}{\diff t}&=F \end{cases} \end{align*} と表すことがで ...
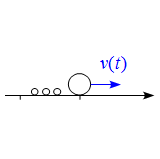
物体の質量が変化する運動
問題 滑らかな水平面上で後方に単位時間当たり$m_0$の物質を噴出しながら 運動する物体がある。物体の初期質量を$M$、初速度を$v_0$とし、噴出物質の速度は 常に0になるように噴出されるものとする。 (1) この運動において運動量が保存されることを示せ。 (2) 時間$t$後の質量$m(t)$を求めよ。 (3) 時間$t$後の速度$v(t)$を求めよ。 (4) 時間$t$後の移動距離$x(t)$を求めよ。 解答 作図をすると (1) 運動方程式は時間$t$後の質量を$m(t)$、速度を$v(t)$とお ...
自由落下運動
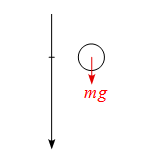
問題 質量$m$の物体を自由落下させる。 以下の問いに答えよ。 但し、重力加速度は$g$とする。 (1) この運動の運動方程式を記述せよ。 (2) この運動において力学的エネルギーが保存していることを運動方程式から導け。 解答 まずは作図をする。 上向きを正に軸を取ると 物体に作用する力を書き込むと (1) 運動方程式は \begin{align*} ma&=-mg\\ m\frac{\diff v}{\diff t}&=-mg \end{align*} となる。 (2) 運動方程式の両辺を$x$で積分す ...
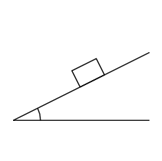
斜面を滑り降りる運動
問題 摩擦がある水平面となす角 $\theta$ の斜面を質量 $m$ の物体がすべり下りる運動を考える。 以下の問いに答えよ。 但し、動摩擦力は $f=\mu_kN$ を用いてよいとする。 (1) この運動の運動方程式を記述せよ。 (2) この運動の加速度 $a$ を求め、この運動が等加速度運動であることを示せ。 解答 まずは作図をする。 この運動は2次元的に動くので、2つの軸を設定する必要がある。 そこで、斜面に平行な軸を$x$とし、斜面に垂直な軸を$y$とする。 物体に作用する力を書き込むと、 $x ...
加速度から速度、変位を求める
問題 $x$軸を運動する質点の加速度が \begin{align*} a(t)=a_0+a_1t \end{align*} で変化している。 $t=0$での速度が$v(0)$であり、位置$x_0$にあったとする。 (1) $t$における質点の速度$v(t)$を求めよ。 (2) $t$における質点の位置$x(t)$を求めよ。 但し、$a_0$, $a_1$は定数であるとする。 解答 (1) 加速度の定義 \begin{align*} \frac{\diff v}{\diff t}=a(t) \end{ali ...