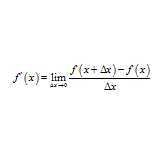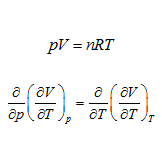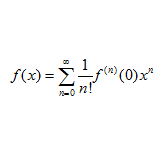物体が滑り出さない条件
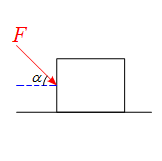
問題 粗い水平面上に置かれた質量$m$の物体に水平と$\alpha$の角をなす方向から 力$F$を加えたとする。物体が滑り出さないための力$F$の条件を求めよ。 但し、静止摩擦係数を$\mu$とする。 解答 $x,y$軸を設定し、物体に作用する力を書き込むと 物体に作用する力は重力$mg$、抗力$R$、加える力$F$となる。 $x,y$軸に合わせて力を分解すると 運動方程式は \begin{align*} \begin{cases} ma_x=F\cos\alpha-f\\ ma_y=N-mg-F\sin ...
微分の定義から導関数を求める
問題 ある関数$f(x)$の導関数$f'(x)$は \begin{align*} f'(x)=\lim_{\Delta x \to \infty}\frac{f(x+\Delta x)-f(x)}{\Delta x} \end{align*} で定義される。 次の関数$f(x)$の導関数$f'(x)$を定義から計算せよ。 (1) $f(x)=2x$ (2) $f(x)=x^n$ (3) $f(x)=\sin x$ (4) $f(x)=\cos x$ 解答 (1) \begin{align*} f'(x)& ...
単振動のエネルギー
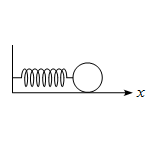
問題 滑らかな水平面上にばねと物体が図のように設置されている。 物体の質量を$m$、ばね定数を$k$とする。 この物体が単振動する時、エネルギー保存則が成立することを運動方程式から導け。 解答 物体に作用する力は ばねの復元力の大きさ$kx$のみである。 従って運動方程式は \begin{align*} m\frac{\diff v}{\diff t}=-kx \end{align*} となる。 両辺を$x$で積分すると \begin{align*} \int m\frac{\diff v}{\diff ...
斜面を滑り下りる運動
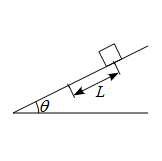
問題 水平面をなす角$\theta$の粗い斜面上の点$\mathrm{A}$から物体を初速$v_0$で斜面に沿って下向きに 打ち出した。物体の質量を$m$、重力加速度を$g$、動摩擦係数を$\mu_k$とする。 点$\mathrm{A}$から距離$L$だけ進んだ点$\mathrm{B}$において以下の問いに答えよ。 (1) 重力がした仕事を求めよ。 (2) 垂直抗力がした仕事を求めよ。 (3) 動摩擦力がした仕事を求めよ。 (4) 点$\mathrm{B}$における速度$v_1$を求めよ。 解答 この運動 ...
偏微分の状態方程式への利用
問題 理想気体の状態方程式は \begin{align*} pV=nRT \qquad(n, R\mbox{は定数)} \end{align*} と表される。 このとき \begin{align*} \frac{\partial}{\partial p}\left(\frac{\partial V}{\partial T}\right)_p=\frac{\partial}{\partial T}\left(\frac{\partial V}{\partial p}\right)_T \end{align* ...
ベクトルの内積
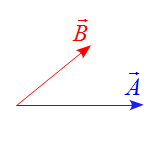
問題 3次元の直交座標系を考える。 ベクトルの成分を \begin{align*} \vec A&=(A_x, A_y, A_z)\\ \vec B&=(B_x, B_y, B_z) \end{align*} とする。 この2つのベクトルの内積が \begin{align*} \vec A\cdot\vec B=A_xB_x+A_yB_y+A_zB_z \end{align*} となることを示せ。 解答 $x$軸, $y$軸, $z$軸方向の単位ベクトルをそれぞれ$\vec i$, $\vec j$, $ ...
マクローリン展開の計算
問題 次の関数$f(x)$をマクローリン級数に展開せよ。 (1) $f(x)=\sin x$ (2) $f(x)=\cos x$ (3) $f(x)=e^x$ 解答 関数$f(x)$のマクローリン展開は \begin{align*} f(x)=\sum_{n=0}^{\infty}\frac{1}{n!}f^{(n)}(0)x^n \end{align*} で与えられる。 (1) \begin{align*} f(0)&=\sin0=0\\ f'(0)&=\cos0=1\\ f''(0)&=-\sin0= ...
密度が一様でない棒の質量
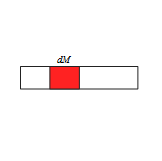
問題 密度が一様でない棒の質量を考える。 この棒の線密度$\rho(x)$が \begin{align*} \rho(x)=\rho_0+\rho_1x \end{align*} で表され、全長が$l$のときこの棒の質量を求めよ。 解答 図に表すと となる。 微笑部分の質量$\diff M$は \begin{align*} \diff M=\rho(x)\diff x \end{align*} と表せる。 よって全質量$M$は \begin{align*} M&=\int_{0}^{l}\rho(x)\d ...
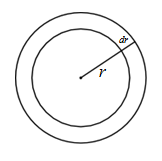
円の面積変化を考える
問題 半径$r$の円がある。その半径を微笑量$\diff r$ $(\diff r\ll r)$だけ変化させたとき、 円の面積の変化$\diff S$はどれだけになるか計算せよ。 解答 円の面積$S$は \begin{align*} S=\pi r^2 \end{align*} である。 $r$が$\diff r$だけ変化したときのSの変化$\diff S$は \begin{align*} \diff S&=\frac{\diff S}{\diff r}\cdot\diff r\\ &=\frac{\di ...