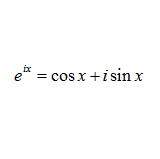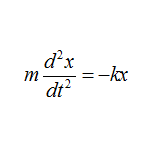力のモーメントの計算
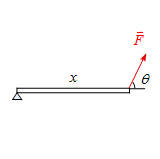
問題 以下の図に力$\vec{F}$が作用した場合の力のモーメント$\vec{M}$を計算し、力のモーメントの大きさ$|\vec{M}|$を求めよ。但し、棒の質量は無視できるものとする。 (1) 棒の長さ$x, \ $棒と作用する力は直交する場合。 (2) 棒の長さ$x, \ $棒と作用する力のなす角は$\theta$の場合。 (3) 棒の長さ$r, \ $作用する力$\vec{F}$の$x,y$成分を$F_x ,\ F_y $とする場合。 解答 (1) 位置ベクトル$\vec{r}_1$を図のように設定 ...
単振動の変位と速度、加速度の関係
問題 単振動の変位 $y(t)$ が \begin{eqnarray*} y(t) = A \sin (\omega t) \end{eqnarray*} と表されているとき以下の問に答えよ。 (1) 速度 $v$ と変位 $y$ の関係を表わせ。 (2) 加速度 $a$ と変位 $y$ の関係を表わせ。 (3) 単振動は運動方程式 $\ddot{y}+\omega ^2 y =0$ を満たすことを示せ。 解答 (1) 速度$v$は \begin{eqnarray*} v = \frac{\diff y} ...
単振り子のエネルギー保存
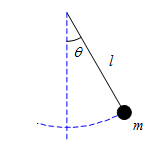
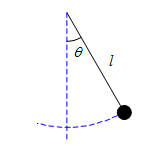
問題 質量$m$の物体が長さ$l$の糸につるされている。 この物体の単振り子運動においてエネルギー保存則が成立することを 運動方程式から導け。 解答 極座標で表した運動方程式は糸の張力を$S$とすると \begin{align*} \begin{cases} ml\left(\frac{\diff\theta}{\diff t}\right)^2=S-mg\cos\theta\\ ml\frac{\diff^2\theta}{\diff t^2}=-mg\sin\theta \end{cases} \en ...
オイラーの公式と加法定理
問題 (1) オイラーの公式 \begin{align*} e^{ix}=\cos x+i\sin x \end{align*} を示せ。 (2) オイラーの公式を使って加法定理を導け。 解答 (1) $e^{ix}$をべき級数展開すると、 \begin{align*} e^{ix}&=1+\frac{ix}{1!}+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+\frac{(ix)^5}{5!}+\frac{(ix)^6}{6!}+\frac ...
単振動の微分方程式
問題 単振動の微分方程式 \begin{align*} m\frac{\diff^2 x}{\diff t^2}=-kx \end{align*} の解を$x(t)=Ce^{\lambda t}$とおいて解け。 但し、$C,\lambda$は定数とする。 解答 $\omega^2=\frac{k}{m}$とおくと、 \begin{align*} \frac{\diff^2 x}{\diff t^2}=-\omega^2x \end{align*} となる。 解である$x(t)=Ce^{\lambda t} ...
単振り子の運動
問題 質量$m$の物体が長さ$l\ $の糸につるされている。 この物体の単振り子運動について以下の問いに答えよ。 (1) 極座標を考えたとき、$r$方向と$\theta$方向の運動方程式を立てよ。 (2) 振れ角$\theta$が十分に小さいとき$\sin\theta\simeq\theta$が成立する。 $\ \ \ \ \ $この時の運動の周期$T$を求めよ。 (3) 物体を十分小さな角$\theta_0$の地点から$t=0$で運動させたとする。 $\ \ \ \ \ $この運動に置いて振れ角$\th ...
極座標の加速度
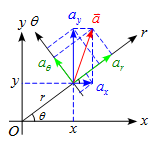
問題 極座標の平面を考える。 加速度$\vec{a}$において$r$方向の加速度$a_r$と$\theta$方向の加速度$a_\theta$を求めよ。 解答 $a_r,a_\theta$を$a_x,a_y$を用いて表すと、 \begin{align*} a_r=&a_x\cos\theta+a_y\sin\theta\\ a_\theta=&-a_x\sin\theta+a_y\cos\theta \end{align*} となる。 ここで \begin{align*} \begin{cases} x=r ...
極座標の速度
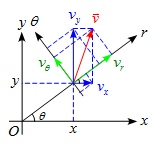
問題 極座標の平面を考える。 速度$\vec{v}$において$r$方向の速度$v_r$と$\theta$方向の速度$v_\theta$を求めよ。 解答 $v_r,v_\theta$を$v_x,v_y$を用いて表すと、 \begin{align*} v_r&=v_x\cos\theta+v_y\sin\theta\\ v_\theta&=-v_x\sin\theta+v_y\cos\theta \end{align*} となる。 ここで \begin{align*} \begin{cases} x=r\co ...
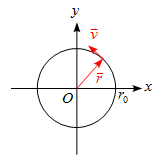
等速円運動の位置、速度、加速度
問題 半径$r_0$、速さ$v_0$で等速円運動をしている物体について 以下の問いに答えよ。 (1) 速度ベクトル$\vec{v}$と位置ベクトル$\vec{r}$が直交していることを示せ。 (2) 速度ベクトル$\vec{v}$と加速度ベクトル$\vec{a}$が直交していることを示せ。 (3) 加速度の大きさ$|\vec{a}|$を求めよ。 解答 直交を示す方法として、$\vec{v}\cdot\vec{r}=0$を示す方法を用いる。 $\vec{r}$と$\vec{v}$のそれぞれをそれ自身と内積を ...