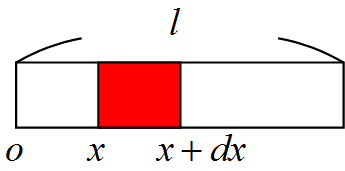問題
密度が一様でない棒の質量を考える。
この棒の線密度$\rho(x)$が
\begin{align*}
\rho(x)=\rho_0+\rho_1x
\end{align*}
で表され、全長が$l$のときこの棒の質量を求めよ。
解答
図に表すと
となる。
微笑部分の質量$\diff M$は
\begin{align*}
\diff M=\rho(x)\diff x
\end{align*}
と表せる。
よって全質量$M$は
\begin{align*}
M&=\int_{0}^{l}\rho(x)\diff x\\
&=\int_{0}^{l}(\rho_0+\rho_1x)\diff x\\
&=\left[\rho_0x+\frac{1}{2}\rho_1x^2\right]_{0}^{l}\\
&=\rho_0l+\frac{1}{2}\rho_1l^2
\end{align*}
となる。