外力が$F(t)$が作用する運動
問題 質量$m$の質点に外力$F(t)$を加え、質点を運動させた。 質点の任意の時刻$t$における速度$v(t)$を求めよ。 但し、$t=0$での速度$v(0)$は$v_0$であるとする。 (1) 外力$F(t)$が、$F(t)=F_0$ のとき (2) 外力$F(t)$が、$F(t)=F_0t$ のとき (3) 外力$F(t)$が、$F(t)=F_0\sin\omega t$ のとき ($F_0$, $\omega$は一定であるとする。) 解答 運動方程式を立てて、速度を計算する。 (1) 運動方程式は ...
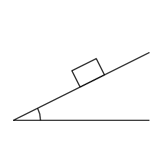
斜面を滑らない条件
問題 水平と角度 $\theta$ をなす荒い斜面上に置かれた物体が滑り出さないための条件を求めよ。 但し、静止摩擦係数を $\mu$ とする。 解答 まずは作図をする。 この運動は2次元的に動くので 2つの軸を設定する必要がある。 そこで、斜面に平行な軸を$x$とし 斜面に垂直な軸を$y$とする。 物体に作用する力を書き込むと、物体の質量を$m$として、 $x$,$y$軸に合わせて力を分解すると 物体が静止している時、 運動方程式はそれぞれの加速度を$a_x$, $a_y$として \begin{alig ...
加法定理を図で示す
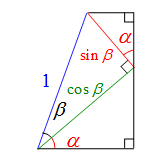
加法定理を図で示す 三角関数の重要公式である「加法定理」は$\sin$と$\cos$の組み合わせで、間違えて覚えてしまうこともあるだろう。加法定理の証明はいくつかあるが、ここでは図で見て視覚的に理解をしておこう。 まず、角度$\beta$を持つ斜辺が$1$の直角三角形を考える。この直角三角形を角度$\alpha$だけ反時計回りに回転させる。そして、底辺と高さと上部を書き加える。 斜辺が$1$なので底辺と高さは$\cos \beta$と$\sin \beta$である。 回転角$\alpha$は図より、上 ...
2次元平面の極座標表示における速度及び加速度を単位ベクトルを使って導出する
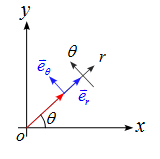
2次元平面の極座標表示における速度$\vec{v}=(v_r, v_\theta)$及び加速度$\vec{a}=(a_r, a_\theta)$を単位ベクトルを使って導出する 速度・加速度の極座標表示 運動の軌道の種類によっては極座標で扱った方が理解しやすいことも多い。 ここでは、2次元平面における極座標表示について単位ベクトルを用いて導出する。。 2次元平面の極座標 図のように、位置ベクトル$\vec{r}$と$x$軸とのなす角を$\theta$とする。 2次元平面の極座標の速度 位置ベクトル$\vec ...
未整理-012
・ ニュートンが初めに提唱した運動方程式の形について ニュートンが初めに提唱した運動方程式の形は \begin{eqnarray} \frac{\diff}{\diff t} (m\vec{v}) =\vec{F} \end{eqnarray} と言われています。 この式は 「$m\vec{v}$ (運動量) の単位時間あたりの変化が力 $\vec{F}$ に等しい」 「運動量$m\vec{v}$が変化すれば, 力$\vec{F}$が作用している」 と解釈することができます。 右辺を計算すると、 \beg ...
未整理-011
・ 等速円運動 〜 位置ベクトル $\vec{r}$, 速度ベクトル $\vec{v}$, 加速度ベクトル$\vec{a}$ の向き 前述の計算より \begin{eqnarray} \vec{r}& =& \left( \begin{array}{cc} x \\ y \\ \end{array} \right) =\left( \begin{array}{cc} r_0 \cos \omega t \\ r_0 \sin \omega t \\ \end{array} \right)\ ...
未整理-010
・ 等速円運動 〜 速度・加速度 半径 $r_0$ 角速度 $\displaystyle \frac{\diff \theta}{\diff t} =\omega \ (\text{一定})$ の等速円運動のモデルについて考える。 速度 $\vec{v}$ を求め、その大きさを計算せよ。 $t=0$ で $(x, y)=(r_0 , 0)$ とすると、ある時刻 $t$ での位置は \begin{eqnarray} x(t) &=& r_0 \cos \omega t\\ y(t) &=& r_0 \sin ...
未整理-009
・ 等速円運動〜角運動量保存 質量 $m$ の物体が半径 $r$ 速さ $v$ の等速円運動をしている。 1. この物体の回転中心まわりの角運動量 $\vec{L}$ の大きさを求めよ。 2. この運動において角運動量が保存していることを示せ。 角運動量 $\vec{L}$ は \begin{eqnarray} \vec{L} &=&\vec{r} \times m\vec{v} \\ &=& r mv \sin \frac{\pi}{2} \vec{e} \ \ (\vec{e} : \vec{r} \ ...
未整理-008
・ 自由落下〜エネルギー保存則 図のように上向きを正に軸を取ると、運動方程式は \begin{eqnarray} ma &=& -mg \\ \\ m \frac{\diff v}{\diff t} &=& -mg \end{eqnarray} ここで、両辺に速度 $\displaystyle v=\frac{\diff x}{\diff t}$ をかけると, \begin{eqnarray} m \frac{\diff v}{\diff t} \color{blue} v &=& -mg \frac{\ ...