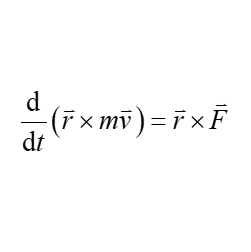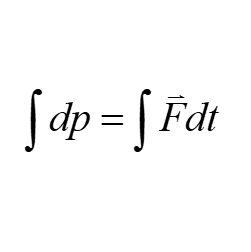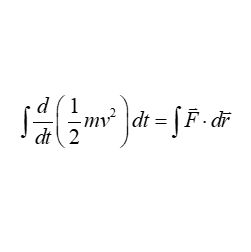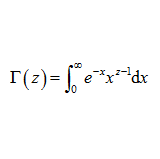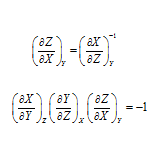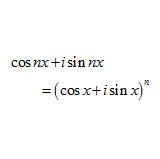kawa

問題 運動方程式$m \vec{a}=\vec{F}$からモーメントと角運動量の関係式を導け。 但し、位置ベクトルを$\vec{r}=(x, y, z)$として扱うとする。   解答 運動方程式$m \vec{a}=\vec{F}$の両辺に左側から位置ベクトル$\vec{r}$の外積をとると、 \begin{eqnarray*} m \vec{a} &=& \vec{F} \\ \\ m \frac{\diff \vec{v}}{\diff t} &=& \vec ...

問題 運動方程式$m \vec{a}=\vec{F}$から力積と運動量の関係式を導け。 但し、位置ベクトルを$\vec{r}=(x, y, z)$として扱うとする。 解答 運動方程式は \begin{eqnarray*} m \vec{a} &=& \vec{F} \\ \\ m \frac{\diff \vec{v}}{\diff t} &=& \vec{F} \\ \\ \frac{\diff }{\diff t} \bigl( m \vec{v} \bigr)&=& \vec{F} \\ \end{ ...

問題 運動方程式$m \vec{a}=\vec{F}$から仕事とエネルギーの関係式を導け。 但し、位置ベクトルを$\vec{r}=(x, y, z)$として扱うとする。 解答 運動方程式は \begin{eqnarray*} m \vec{a} &=& \vec{F} \\ \\ m \frac{\diff \vec{v}}{\diff t} &=& \vec{F} \end{eqnarray*} と表される。 ここで、両辺に$\diff \vec{r}$の内積を取って積分すると \begin{eqnar ...

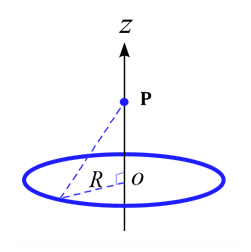
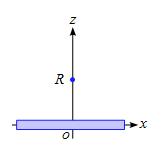
問題 図のような$z$軸を中心軸に持つ半径$R$のリング状に線密度$\rho$で電荷が一様に分布している。 線の太さは無視できるものとして、以下の問いに答えよ。 (1) OPの距離を$z$とすると、点Pでの電場の大きさを求めよ。 (2) OPの距離を$z$とすると、点Pでの電位の大きさを求めよ。 但し、電位の基準は無限遠とする。 解答 (1) クーロンの法則を適用するために、リングの一部を微小部分$\diff s$と設定する。この微小部分$\diff s$が作る電場$\diff E$を計算し、全区間に対し ...

問題 ガンマ関数$\Gamma (z)$は \begin{eqnarray*} \Gamma (z) = \int_{0}^{\infty} e^{-x} x^{z-1} \diff x \end{eqnarray*} で定義される。 以下の問いに答えよ。 (1) $\Gamma (1)$の値を計算せよ。 (2) $\Gamma \left( \displaystyle \frac{1}{2} \right)$の値を計算せよ。 (3) $\Gamma (z+1) = z\Gamma (z)$を示せ。 (4 ...

問題 以下の関係式を導出せよ。 (1) $\displaystyle \left( \frac{\partial Z}{\partial X} \right)_Y = \left( \frac{\partial X}{\partial Z} \right)^{-1}_Y$ (2) $\displaystyle \left( \frac{\partial X}{\partial Y} \right)_Z \left( \frac{\partial Y}{\partial Z} \right)_X \left ...

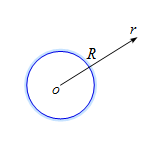
問題 一様な面密度$\sigma$で球表面に帯電した半径$R$の球がある。以下の問いに答えよ。 (1) この球の中心からの距離$r \ (\ge R)$での電場の大きさ$E(r)$を求めよ。 (2) この球の中心からの距離$r \ (\le R)$での電場の大きさ$E(r)$を求めよ。 (3) 球の内外につくる静電場を距離$r$の関数としてグラフを書け。 解答 (1) $r \ (\ge R)$の場合、ガウスの法則を適用する閉曲面を図のように半径$r$の球(赤の点線)を想定する。 このとき、閉曲面内の電気 ...

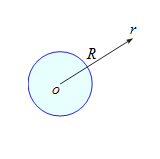
問題 一様な電荷密度$\rho$で帯電した半径$R$の球がある。以下の問いに答えよ。 (1) この球の中心からの距離$r \ (\ge R)$での電場の大きさ$E(r)$を求めよ。 (2) この球の中心からの距離$r \ (\le R)$での電場の大きさ$E(r)$を求めよ。 (3) 球の内外につくる静電場を距離$r$の関数としてグラフを書け。 解答 (1) $r \ (\ge R)$の場合、ガウスの法則を適用する閉曲面を図のように半径$r$の球(赤の点線)を想定する。 このとき、閉曲面内の電気量$Q$は ...

問題 単位長さあたりの電気量(線密度)が$\rho$である無限に長い直線上に電荷が分布している。 以下の方法を用いて直線から距離$R$の位置での電場を求めよ。但し、線の太さは無視できるものとする。 (1) クーロンの法則を用いて電場を求めよ。 (2) ガウスの法則を用いて電場を求めよ。 解答 (1) クーロンの法則を適用するために、直線の一部を微小部分$\diff x$を設定する。この微小部分$\diff x$が作る電場を計算し、全区間に対して積分を行うとする。 微小部分$\diff x$の電気量$\di ...

問題 オイラーの公式$e^{ix}=\cos x +i\sin x$を用いてド・モアブルの定理 \begin{eqnarray*} \cos nx + i \sin nx = (\cos x +i\sin x)^n \end{eqnarray*} を導出せよ。 解答 $e^{inx}$を考えると、 \begin{eqnarray*} e^{inx} &=& (e^{ix})^n \\ \\ &=& (\cos x +i\sin x)^n \\ \end{eqnarray*} となる。 一方 \begin{ ...