加法定理を図で示す
三角関数の重要公式である「加法定理」は$\sin$と$\cos$の組み合わせで、間違えて覚えてしまうこともあるだろう。加法定理の証明はいくつかあるが、ここでは図で見て視覚的に理解をしておこう。
まず、角度$\beta$を持つ斜辺が$1$の直角三角形を考える。この直角三角形を角度$\alpha$だけ反時計回りに回転させる。そして、底辺と高さと上部を書き加える。

- 斜辺が$1$なので底辺と高さは$\cos \beta$と$\sin \beta$である。
- 回転角$\alpha$は図より、上部の直角三角形の下部の角も$\alpha$となる。
それぞれの辺、$1$, $\cos \beta$ , $\sin \beta$に対して底辺と高さを計算すると
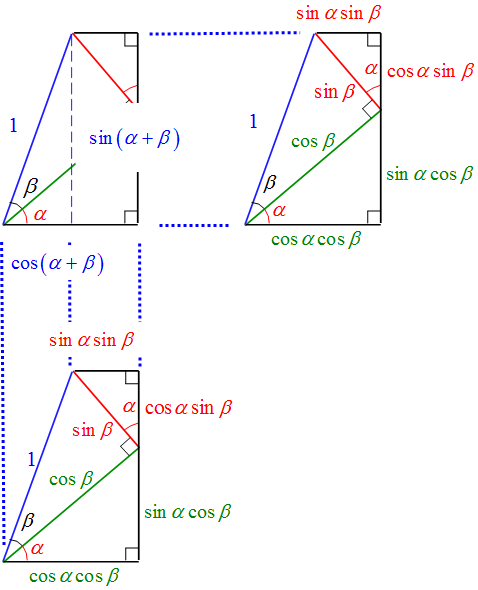
斜辺の$1$に対して
- 角度は$\alpha + \beta$となる。
- 底辺は$\cos (\alpha + \beta)$となる。
- 高さは$\sin (\alpha + \beta)$となる。
底辺の$\cos \beta$を斜面に持つ下部の直角三角形に対して
- 角度は$\alpha$となる。
- 底辺は$\cos \alpha \cos \beta$となる。
- 高さは$\sin \alpha \cos \beta$となる。
高さの$\sin \beta$を斜面に持つ上部の直角三角形に対して
- 角度は$\alpha$となる。
- 底辺は$\cos \alpha \sin \beta$となる。
- 高さは$\sin \alpha \sin \beta$となる。
従って、図より$\sin (\alpha + \beta)$は台形の高さであり、
\begin{eqnarray*}
\color{blue}{\sin (\alpha + \beta)} = \color{green}{\sin \alpha \cos \beta} + \color{red}{\cos \alpha \sin \beta}
\end{eqnarray*}
となる。
また、図より$\cos (\alpha + \beta)$は台形の底辺から上辺を引いた部分であるから
\begin{eqnarray*}
\color{blue}{\cos (\alpha + \beta)} = \color{green}{\cos \alpha \cos \beta} - \color{red}{\sin \alpha \sin \beta}
\end{eqnarray*}
となる。
図を見ればそれぞれの加法定理が一目瞭然である。