斜面を滑り降りる運動

問題

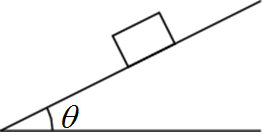
摩擦がある水平面となす角 $\theta$ の斜面を質量 $m$ の物体がすべり下りる運動を考える。
以下の問いに答えよ。
但し、動摩擦力は $f=\mu_kN$ を用いてよいとする。

(1) この運動の運動方程式を記述せよ。

(2) この運動の加速度 $a$ を求め、この運動が等加速度運動であることを示せ。

解答

まずは作図をする。

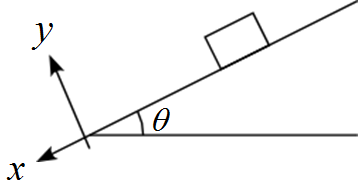
この運動は2次元的に動くので、2つの軸を設定する必要がある。
そこで、斜面に平行な軸を$x$とし、斜面に垂直な軸を$y$とする。

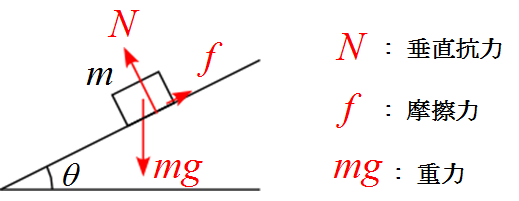
物体に作用する力を書き込むと、

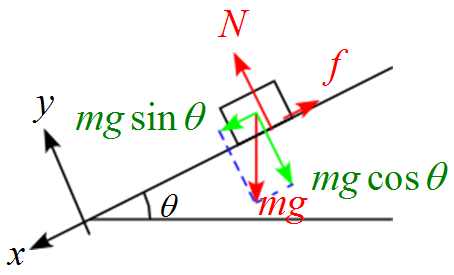
$x$, $y$軸に合わせて力を分解すると

(1) 運動方程式はそれぞれの加速度を$a_x$, $a_y$として
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-f&\\
ma_y=N-mg\cos\theta&
\end{cases}
\end{align*}
と表すことができる。$a_y=0$, $f=\mu_kN$より
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-\mu_kN&\\
0=N-mg\cos\theta&
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-\mu_kN&\\
N=mg\cos\theta&
\end{cases}
\end{align*}
\begin{align*}
ma_x=mg\sin\theta-\mu_kmg\cos\theta
\end{align*}
となる。

(2) 運動方程式より
\begin{align*}
a=a_x&=g\sin\theta-\mu_kg\cos\theta\\
&=g(\sin\theta-\mu_k\cos\theta)
\end{align*}
となる。
$g$, $\theta$, $\mu_k$は定数であるので$a$は定数である。
従ってこの運動は等加速度運動である。