問題
質量を持つ2つの物体の間には万有引力が作用する。
このことから地球の重力$mg$を求めるとする。
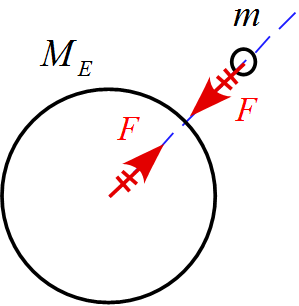
(1) 地球の半径を$R_\mathrm{E}$、地球の質量を$M_\mathrm{E}$、物体の質量を$m$とし、
地表から物体までの高さ$h$は$R_\mathrm{E}$に比べて極めて小さく、無視できるものとする。
万有引力の法則
\begin{align*}
F=G\frac{m_1m_2}{r^2}
\end{align*}
から重力加速度$g$を表せ。
(2) $G=6.67\times10^{-11}$[$\mathrm{Nm^2/kg^2}$],$R_\mathrm{E}=6.38\times10^6$[$\mathrm{m}$],
$M_\mathrm{E}=5.98\times10^{24}$[$\mathrm{kg}$]として、$g$の値を計算せよ。
解答
(1) 万有引力の法則より、
\begin{align*}
F=G\frac{m_1m_2}{r^2}&=G\frac{M_\mathrm{E}\cdot m}{R_\mathrm{E}^2}\\
&=\frac{GM_\mathrm{E}}{R_\mathrm{E}^2}\cdot m
\end{align*}
また、重力$f_g=mg$と表せることから
\begin{align*}
g=\frac{GM_\mathrm{E}}{R_\mathrm{E}^2}\
\end{align*}
と表される。
(2)
\begin{align*}
g&=\frac{6.67\times10^{-11}[\mathrm{Nm^2/kg^2}]\times5.98\times10^{24}[\mathrm{kg}]}{(6.38\times10^6[\mathrm{m}])^2}\\
&=9.7990 \ \mathrm{[m/s^2]}\\
&\simeq9.80 \ \mathrm{[m/s^2]}
\end{align*}
となる。
(与えられた有効数字に合わせる)