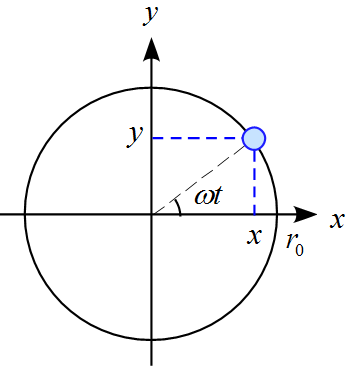
・ 等速円運動 〜 位置ベクトル $\vec{r}$, 速度ベクトル $\vec{v}$, 加速度ベクトル$\vec{a}$ の向き
\begin{eqnarray}
\vec{r}& =& \left(
\begin{array}{cc}
x \\
y \\
\end{array}
\right)
=\left(
\begin{array}{cc}
r_0 \cos \omega t \\
r_0 \sin \omega t \\
\end{array} \right)\\
\end{eqnarray}
\begin{eqnarray}
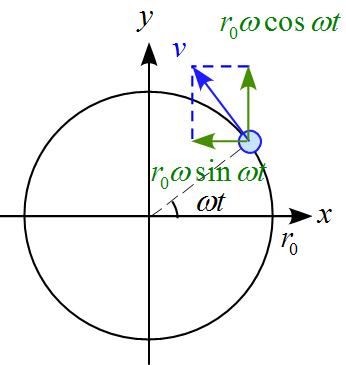
\vec{v} &=& \left(
\begin{array}{cc}
v_x \\
v_y \\
\end{array}
\right)
=\left(
\begin{array}{cc}
- r_0 \omega \sin \omega t \\
r_0 \omega \cos \omega t \\
\end{array} \right) \\
\end{eqnarray}
\begin{eqnarray}
\vec{a}& =& \left(
\begin{array}{cc}
a_x \\
a_y \\
\end{array}
\right)
=\left(
\begin{array}{cc}
- r_0 \omega^2 \cos \omega t \\
- r_0 \omega^2 \sin \omega t \\
\end{array} \right)
\end{eqnarray}
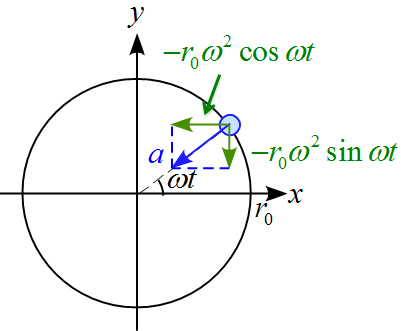
であるから
\begin{eqnarray}
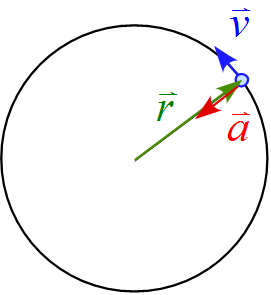
\vec{r} \perp \vec{v}\\
\\
\vec{r} \parallel \vec{a}\\
\end{eqnarray}
となることがわかる。
\begin{eqnarray}
&\vec{r}&\ \mbox{と}\ \vec{v}\ \ (\mbox{なす角}\ 90^{\circ})\\
\\
&\vec{r}&\ \mbox{と}\ \vec{a}\ \mbox{は逆向き}\ (\mbox{なす角}\ 180^{\circ})\\
\end{eqnarray}
Checkしておきましょう。
注) このページは物理な内容を淡々と描くものです。過度な期待はしないで下さい。