・ 等速円運動 〜 速度・加速度
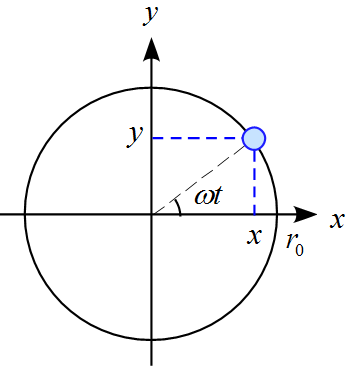
半径 $r_0$ 角速度 $\displaystyle \frac{\diff \theta}{\diff t} =\omega \ (\text{一定})$ の等速円運動のモデルについて考える。
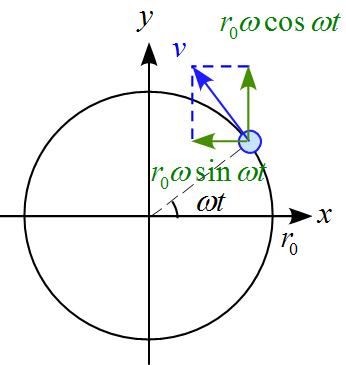
速度 $\vec{v}$ を求め、その大きさを計算せよ。
$t=0$ で $(x, y)=(r_0 , 0)$ とすると、ある時刻 $t$ での位置は
\begin{eqnarray}
x(t) &=& r_0 \cos \omega t\\
y(t) &=& r_0 \sin \omega t\\
\end{eqnarray}
と表される。
よって、速度 $v$ は
\begin{eqnarray}
v_x &=& \frac{\diff }{\diff t} \left( r_0 \cos \omega t \right) = - r_0 \omega \sin \omega t \\
\\
v_y &=& \frac{\diff }{\diff t} \left( r_0 \sin \omega t \right) = r_0 \omega \cos \omega t\\
\end{eqnarray}
となるので、
\begin{eqnarray}
\vec{v} = \left(
\begin{array}{cc}
v_x \\
v_y \\
\end{array}
\right)
=\left(
\begin{array}{cc}
- r_0 \omega \sin \omega t \\
r_0 \omega \cos \omega t \\
\end{array} \right)
\end{eqnarray}
従って、
\begin{eqnarray}
v=\sqrt{v_x^2 +v_y^2} &=& \sqrt{(- r_0 \omega \sin \omega t)^2+(r_0 \omega \cos \omega t)^2}\\
\\
&=& \sqrt{ r_0^2 \omega ^2 \sin ^2\omega t+r_0^2 \omega ^2 \cos ^2\omega t } \\
\\
&=& \sqrt{r_0^2 \omega ^2 (\sin ^2\omega t +\cos ^2 \omega t)} \\
\\
&=& \sqrt{r_0^2 \omega ^2}\\
\\
&=& r_0 \omega
\end{eqnarray}
となる。
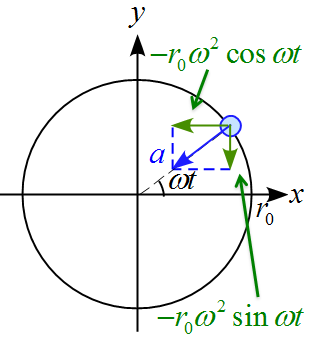
速度 $\vec{a}$ を求め、その大きさを計算せよ。
同様に、加速度については
\begin{eqnarray}
a_x &=& \frac{\diff }{\diff t} \left( - r_0 \omega \sin \omega t \right) = - r_0 \omega ^2 \cos \omega t \\
\\
a_y &=& \frac{\diff }{\diff t} \left( r_0 \omega \cos \omega t \right) = - r_0 \omega ^2 \sin \omega t\\
\end{eqnarray}
となるので、
\begin{eqnarray}
\vec{a} = \left(
\begin{array}{cc}
a_x \\
a_y \\
\end{array}
\right)
=\left(
\begin{array}{cc}
- r_0 \omega^2 \cos \omega t \\
- r_0 \omega^2 \sin \omega t \\
\end{array} \right)
\end{eqnarray}
従って、
\begin{eqnarray}
a=\sqrt{a_x^2 +a_y^2} &=& \sqrt{(- r_0 \omega^2 \cos \omega t)^2+(- r_0 \omega^2 \sin \omega t)^2}\\
\\
&=& \sqrt{ r_0^2 \omega ^4 \cos ^2\omega t+r_0^2 \omega ^4 \sin ^2\omega t }\\
\\
&=& \sqrt{r_0^2 \omega ^4 (\cos ^2\omega t +\sin ^2 \omega t)} \\
\\
&=& \sqrt{r_0^2 \omega ^4}\\
\\
&=& r_0 \omega^2
\end{eqnarray}
となる。
角速度 $\omega$ が定数なので微分の計算は比較的楽でいいすね。
注) このページは物理な内容を淡々と描くものです。過度な期待はしないで下さい。