・ 等速円運動〜角運動量保存
質量 $m$ の物体が半径 $r$ 速さ $v$ の等速円運動をしている。
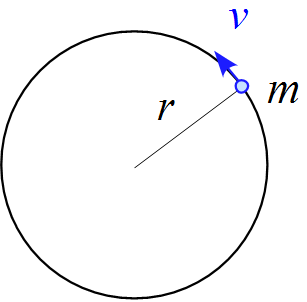
1. この物体の回転中心まわりの角運動量 $\vec{L}$ の大きさを求めよ。
2. この運動において角運動量が保存していることを示せ。
角運動量 $\vec{L}$ は
\begin{eqnarray}
\vec{L} &=&\vec{r} \times m\vec{v} \\
&=& r mv \sin \frac{\pi}{2} \vec{e} \ \ (\vec{e} : \vec{r} \perp \vec{e} ,\ \vec{v} \perp \vec{e} \ \mbox{となる方向の単位ベクトル}) \\
&=& r mv \ \vec{e} \\
|\vec{L}| &=& mrv
\end{eqnarray}
角運動量の時間変化は
\begin{eqnarray}
\frac{\diff \vec{L}}{\diff t} &=&\frac{\diff}{\diff t} \left( \vec{r} \times m\vec{v} \right)\\
\\
&=& \frac{\diff \vec{r}}{\diff t} \times m\vec{v} + \vec{r} \times \frac{\diff}{\diff t} \left( m\vec{v} \right) \\
\\
&=& \vec{v} \times m\vec{v} + \vec{r} \times m\frac{\diff \vec{v}}{\diff t} \\
\\
&=& m \vec{v} \times \vec{v} + \vec{r} \times m \vec{a} \\
\\
&=&0
\end{eqnarray}
従って, 角運動量は時間的に変化せず, 保存している。
補足
外積について
\begin{eqnarray}
\vec{A} \times \vec{B} = |\vec{A}| |\vec{B}| \sin \theta \ \vec{e}\\
\end{eqnarray}
を利用した。
この問題では $\vec{r}$ と $\vec{v}$ のなす角$\theta$は $\displaystyle 90^{\circ} =\frac{\pi}{2} $ である。
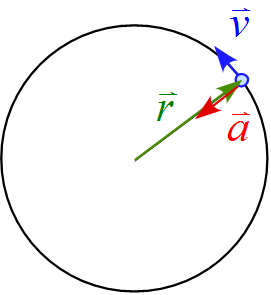
また, 2つのベクトルが並行の場合, 即ち, $\theta = 0^{\circ} \mbox {or} \ 180^{\circ}$ の場合は $\sin \theta = 0$ となるので外積も $0$ となる。
注) このページは物理な内容を淡々と描くものです。過度な期待はしないで下さい。