問題
極座標の平面を考える。
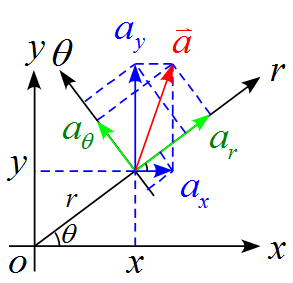
加速度$\vec{a}$において$r$方向の加速度$a_r$と$\theta$方向の加速度$a_\theta$を求めよ。
解答
$a_r,a_\theta$を$a_x,a_y$を用いて表すと、
\begin{align*}
a_r=&a_x\cos\theta+a_y\sin\theta\\
a_\theta=&-a_x\sin\theta+a_y\cos\theta
\end{align*}
となる。
ここで
\begin{align*}
\begin{cases}
x=r\cos\theta\\
y=r\sin\theta
\end{cases}
\end{align*}
であるので
\begin{align*}
v_x=\frac{\diff x}{\diff t}=\frac{\diff r}{\diff t}\cos\theta-r\sin\theta\frac{\diff\theta}{\diff t}\\
v_y=\frac{\diff y}{\diff t}=\frac{\diff r}{\diff t}\sin\theta+r\cos\theta\frac{\diff\theta}{\diff t}
\end{align*}
となる。さらに$t$で微分すると、
\begin{align*}
a_x=&\frac{\diff}{\diff t}\left(\frac{\diff r}{\diff t}\cos\theta-r\sin\theta\frac{\diff\theta}{\diff t}\right)\\
=&\frac{\diff}{\diff t}\left(\frac{\diff r}{\diff t}\right)\cos\theta+\frac{\diff r}{\diff t}\frac{\diff}{\diff t}(\cos\theta)-\left[\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}+r\frac{\diff}{\diff t}\left(\sin\theta\frac{\diff\theta}{\diff t}\right)\right]\\
=&\frac{\diff ^2 r}{\diff t^2}\cos\theta+\frac{\diff r}{\diff t}\left(-\sin\theta\frac{\diff\theta}{\diff t}\right)-\left[\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}+r\left\{\frac{\diff}{\diff t}(\sin\theta)\frac{\diff\theta}{\diff t}+\sin\theta\frac{\diff}{\diff t}\frac{\diff\theta}{\diff t}\right\}\right]\\
=&\frac{\diff ^2 r}{\diff t^2}\cos\theta-\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}-\left[\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}+r\left(\cos\theta\frac{\diff\theta}{\diff t}\right)\frac{\diff\theta}{\diff t}+r\sin\theta\frac{\diff^2 \theta}{\diff t^2}\right]\\
=&\frac{\diff ^2 r}{\diff t^2}\cos\theta-2\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}-r\cos\theta\left(\frac{\diff\theta}{\diff t}\right)^2-r\sin\theta\frac{\diff^2 \theta}{\diff t^2}\\
a_y=&\frac{\diff}{\diff t}\left(\frac{\diff r}{\diff t}\sin\theta+r\cos\theta\frac{\diff\theta}{\diff t}\right)\\
=&\frac{\diff}{\diff t}\left(\frac{\diff r}{\diff t}\right)\sin\theta+\frac{\diff r}{\diff t}\frac{\diff}{\diff t}(\sin\theta)+\frac{\diff r}{\diff t}\left(\cos\theta\frac{\diff\theta}{\diff t}\right)+r\frac{\diff}{\diff t}\left(\cos\theta\frac{\diff\theta}{\diff t}\right)\\
=&\frac{\diff ^2 r}{\diff t^2}\sin\theta+\frac{\diff r}{\diff t}\left(\cos\theta\frac{\diff\theta}{\diff t}\right)+\frac{\diff r}{\diff t}\cos\theta\frac{\diff\theta}{\diff t}+r\left[\frac{\diff}{\diff t}(\cos\theta)\frac{\diff\theta}{\diff t}+\cos\theta\frac{\diff}{\diff t}\left(\frac{\diff\theta}{\diff t}\right)\right]\\
=&\frac{\diff ^2 r}{\diff t^2}\sin\theta+2\frac{\diff r}{\diff t}\cos\theta\frac{\diff\theta}{\diff t}+r\left[\left(-\sin\theta\frac{\diff\theta}{\diff t}\right)\frac{\diff\theta}{\diff t}+\cos\theta\frac{\diff^2 \theta}{\diff t^2}\right]\\
=&\frac{\diff ^2 r}{\diff t^2}\sin\theta+2\frac{\diff r}{\diff t}\cos\theta\frac{\diff\theta}{\diff t}-r\sin\theta\left(\frac{\diff\theta}{\diff t}\right)^2+r\cos\theta\frac{\diff^2 \theta}{\diff t^2}
\end{align*}
となる。
これらを$a_r,a_\theta$の式に代入すると、
\begin{align*}
a_r=&a_x\cos\theta+a_y\sin\theta\\
=&\left[\frac{\diff ^2 r}{\diff t^2}\cos\theta-2\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}-r\cos\theta\left(\frac{\diff\theta}{\diff t}\right)^2-r\sin\theta\frac{\diff^2 \theta}{\diff t^2}\right]\cos\theta+\\
&\left[\frac{\diff ^2 r}{\diff t^2}\sin\theta+2\frac{\diff r}{\diff t}\cos\theta\frac{\diff\theta}{\diff t}-r\sin\theta\left(\frac{\diff\theta}{\diff t}\right)^2+r\cos\theta\frac{\diff^2 \theta}{\diff t^2}\right]\sin\theta\\
=&\frac{\diff ^2 r}{\diff t^2}\cos^2\theta-2\frac{\diff r}{\diff t}\sin\theta\cos\theta\frac{\diff\theta}{\diff t}-r\cos^2\theta\left(\frac{\diff\theta}{\diff t}\right)^2-r\sin\theta\cos\theta\frac{\diff^2 \theta}{\diff t^2}+\\
&\frac{\diff ^2 r}{\diff t^2}\sin^2\theta+2\frac{\diff r}{\diff t}\sin\theta\cos\theta\frac{\diff\theta}{\diff t}-r\sin^2\theta\left(\frac{\diff\theta}{\diff t}\right)^2+r\sin\theta\cos\theta\frac{\diff^2 \theta}{\diff t^2}\\
=&\frac{\diff ^2 r}{\diff t^2}(\cos^2\theta+\sin^2\theta)-r\left(\frac{\diff\theta}{\diff t}\right)^2(\cos^2\theta+\sin^2\theta)\\
=&\frac{\diff ^2 r}{\diff t^2}-r\left(\frac{\diff\theta}{\diff t}\right)^2\\
a_\theta=&-a_x\sin\theta+a_y\cos\theta\\
=&-\left[\frac{\diff ^2 r}{\diff t^2}\cos\theta-2\frac{\diff r}{\diff t}\sin\theta\frac{\diff\theta}{\diff t}-r\cos\theta\left(\frac{\diff\theta}{\diff t}\right)^2-r\sin\theta\frac{\diff^2 \theta}{\diff t^2}\right]\sin\theta+\\
&\left[\frac{\diff ^2 r}{\diff t^2}\sin\theta+2\frac{\diff r}{\diff t}\cos\theta\frac{\diff\theta}{\diff t}-r\sin\theta\left(\frac{\diff\theta}{\diff t}\right)^2+r\cos\theta\frac{\diff^2 \theta}{\diff t^2}\right]\cos\theta\\
=&-\frac{\diff ^2 r}{\diff t^2}\sin\theta\cos\theta+2\frac{\diff r}{\diff t}\sin^2\theta\frac{\diff\theta}{\diff t}+r\sin\theta\cos\theta\left(\frac{\diff\theta}{\diff t}\right)^2+r\sin^2\theta\frac{\diff^2 \theta}{\diff t^2}+\\
&\frac{\diff ^2 r}{\diff t^2}\sin\theta\cos\theta+2\frac{\diff r}{\diff t}\cos^2\theta\frac{\diff\theta}{\diff t}-r\sin\theta\cos\theta\left(\frac{\diff\theta}{\diff t}\right)^2+r\cos^2\theta\frac{\diff^2 \theta}{\diff t^2}\\
=&2\frac{\diff r}{\diff t}\frac{\diff\theta}{\diff t}(\cos^2\theta+\sin^2\theta)+r\frac{\diff^2\theta}{\diff t^2}(\cos^2\theta+\sin^2\theta)\\
=&2\frac{\diff r}{\diff t}\frac{\diff\theta}{\diff t}+r\frac{\diff^2\theta}{\diff t^2}\\
=&\frac{1}{r}\frac{\diff}{\diff t}\left(r^2\frac{\diff\theta}{\diff t}\right)
\end{align*}
従って
\begin{align*}
a_r=&\frac{\diff ^2 r}{\diff t^2}-r\left(\frac{\diff\theta}{\diff t}\right)^2\\
a_\theta=&\frac{1}{r}\frac{\diff}{\diff t}\left(r^2\frac{\diff\theta}{\diff t}\right)
\end{align*}
となる。