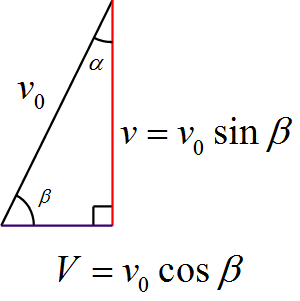問題
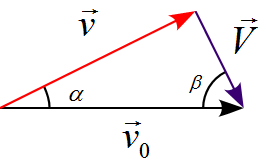
質量が等しい2つの質点A, Bがある。
静止しているBに速度$v_0$でAが衝突し、その後、図のようになす角$\alpha$, $\beta$で、
速度$v$, $V$でそれぞれ運動した。
この衝突は弾性衝突であり、衝突の前後で運動エネルギーは不変であるとする。
(1) 角$\alpha+\beta$を求めよ。
(2) 速度比$\dfrac{v}{V}$を$\beta$を用いて表せ。
解答
(1) 運動量保存則より
\begin{align*}
m\vec{v_0}=m\vec{v}+m\vec{V}
\end{align*}
であるから
\begin{align*}
\vec{v_0}=\vec{v}+\vec{V}
\end{align*}
となる。
これを図で表すと、
となる。
一方、衝突の前後でエネルギーのロスが無いのでエネルギー保存が成り立ち、
\begin{align*}
\frac{1}{2}mv_0^2&=\frac{1}{2}mv^2+\frac{1}{2}mV^2\\
v_0^2&=v^2+V^2
\end{align*}
となる。
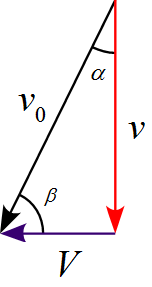
ここで図を書き直すと、
となり、$v_0$を斜辺とする直角三角形を表している。
従って
\begin{align*}
\alpha+\beta=90^\circ
\end{align*}
となる。
(2) 図より$v$, $V$を$\beta$を用いて表すと
\begin{align*}
\begin{cases}
v&=v_0\sin\beta\\
V&=v_0\cos\beta
\end{cases}
\end{align*}
であるから、
\begin{align*}
\frac{v}{V}&=\frac{v_0\sin\beta}{v_0\cos\beta}\\
&=\tan\beta
\end{align*}
となる。