物体の質量が変化する運動

問題

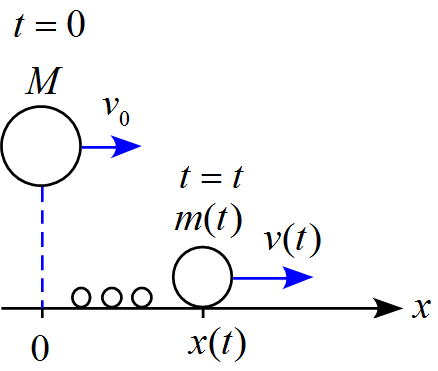
滑らかな水平面上で後方に単位時間当たり$m_0$の物質を噴出しながら
運動する物体がある。物体の初期質量を$M$、初速度を$v_0$とし、噴出物質の速度は
常に0になるように噴出されるものとする。

(1) この運動において運動量が保存されることを示せ。

(2) 時間$t$後の質量$m(t)$を求めよ。

(3) 時間$t$後の速度$v(t)$を求めよ。

(4) 時間$t$後の移動距離$x(t)$を求めよ。

解答

作図をすると

(1) 運動方程式は時間$t$後の質量を$m(t)$、速度を$v(t)$とおくと、

$$\begin{align*} \frac{\diff}{\diff t}\Bigl(m(t)v(t)\Bigr)=F \end{align*}$$
と表すことができる
この運動では外部から力が作用していないので、
$$\begin{align*} \frac{\diff}{\diff t}\Bigl(m(t)v(t)\Bigr)=0 \end{align*}$$
となる。
従って運動量$m(t)v(t)$は時間的に変化しないので
運動量は保存している。

(2) 単位時間あたり$m_0$の質量が減っていくので$t$後には

$$\begin{align*} \mbox{減った質量}=m_0t \end{align*}$$
と表すことができる。
よって$t$後の質量$m(t)$は
$$\begin{align*} m(t)=M-m_0t \end{align*}$$
となる。

(3) 運動量が保存しているので、

$$\begin{align*} m(t)v(t)=Mv_0 \end{align*}$$
である。
よって
$$\begin{align*} m(t)v(t)&=Mv_0\\ v(t)&=\frac{M}{m(t)}v_0\\ &=\frac{M}{M-m_0t}v_0 \end{align*}$$
となる。

(4) $v(t)$の両辺を時間0から$t$まで$t$で積分すると、

$$\begin{align*} x(t)&=\int_{0}^{t}v(t)\diff t\\ &=\int_{0}^{t}\frac{Mv_0}{M-m_0t}v_0\diff t\\ &=Mv_0\int_{0}^{t}\frac{1}{M-m_0t}v_0\diff t\\ &=Mv_0\left[-\frac{1}{m_0}\cdot\log(M-m_0t)\right]_{0}^{t}\\ &=-\frac{Mv_0}{m_0}\Bigl[\log(M-m_0t)\Bigr]_{0}^{t}\\ &=-\frac{Mv_0}{m_0}\Bigl\{\log(M-m_0t)-\log(M-m_0\cdot0)\Bigr\}\\ &=-\frac{Mv_0}{m_0}\Bigl\{\log(M-m_0t)-\log M\Bigr\}\\ &=-\frac{Mv_0}{m_0}\log\frac{M-m_0t}{M} \end{align*}$$
となる。