問題
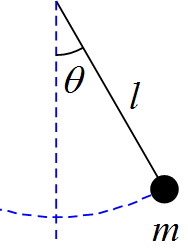
質量$m$の物体が長さ$l$の糸につるされている。
この物体の単振り子運動においてエネルギー保存則が成立することを
運動方程式から導け。
解答
極座標で表した運動方程式は糸の張力を$S$とすると
\begin{align*}
\begin{cases}
ml\left(\frac{\diff\theta}{\diff t}\right)^2=S-mg\cos\theta\\
ml\frac{\diff^2\theta}{\diff t^2}=-mg\sin\theta
\end{cases}
\end{align*}
となる。
ここで、物体の速度$v$は
\begin{align*}
v=l\frac{\diff\theta}{\diff t}
\end{align*}
であるから、
\begin{align*}
\frac{\diff\theta}{\diff t}&=\frac{v}{l}\\
\frac{\diff^2\theta}{\diff t^2}&=\frac{1}{l}\frac{\diff v}{\diff t}
\end{align*}
と表される。
運動方程式
\begin{align*}
ml\frac{\diff^2\theta}{\diff t^2}=-mg\sin\theta
\end{align*}
において両辺に$v=l\frac{\diff\theta}{\diff t}$をかけると
\begin{align*}
ml\frac{\diff^2\theta}{\diff t^2}\cdot v&=-mg\sin\theta\cdot l\frac{\diff\theta}{\diff t}\\
ml\frac{1}{l}\frac{\diff v}{\diff t}v&=-mgl\sin\theta\frac{\diff\theta}{\diff t}\\
mv\frac{\diff v}{\diff t}&=-mgl\sin\theta\frac{\diff\theta}{\diff t}\\
\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2\right)&=\frac{\diff}{\diff t}\left(mgl\cos\theta\right)\\
\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2-mgl\cos\theta\right)&=0
\end{align*}
となる。
ここで( )内に定数$mgl$を加えると
\begin{align*}
\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2-mgl\cos\theta+mgl\right)&=0\\
\frac{\diff}{\diff t}\left[\frac{1}{2}mv^2+mgl(1-\cos\theta)\right]&=0
\end{align*}
となる。
この式において、第1項の$\frac{1}{2}mv^2$は運動エネルギーを表し、
第2項の$mgl(1-\cos\theta)$は位置エネルギーを表している。
従って、運動エネルギーと位置エネルギーの和である力学的エネルギーが
時間的に変化しないことを表している。
即ち、エネルギー保存則が成立している。
補足
定数$mgl$を加えたのは最下点を位置エネルギーの基準に設定する為である。(定数なので微分の中に加えても等式は成立する)
最下点$\theta=0$において位置エネルギー$U$は
\begin{align*}
U_{\theta=0}&=mgl(1-\cos0)\\
&=mgl(1-1)\\
&=0
\end{align*}
である。
又、
\begin{align*}
\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2-mgl\cos\theta\right)&=0
\end{align*}
において、2つの点を考えた場合
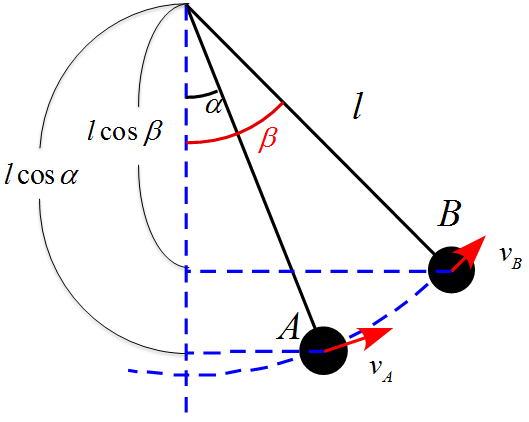
A地点 $\theta=\alpha,v=v_\mathrm{A}$
B地点 $\theta=\beta,v=v_\mathrm{B}$
2つの地点において
\begin{align*}
\frac{1}{2}mv_\mathrm{A}^2-mgl\cos\alpha&=\frac{1}{2}mv_\mathrm{B}^2-mgl\cos\beta\\
\frac{1}{2}m(v_\mathrm{A}^2-v_\mathrm{B}^2)&=mgl(\cos\alpha-\cos\beta)
\end{align*}
となり、「運動エネルギーの変化は物体の働く仕事に等しい」ことがわかる。