単振動の変位、速度、加速度

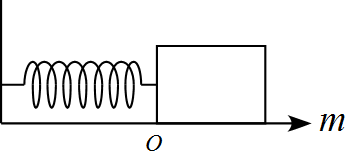
問題

なめらかな水平面上に壁からばねが取り付けれられている。
ばねは自然長の状態で静止しているとする。

$t=0$で初速度$v_0$を壁向きに与えると、物体は単振動した。
物体の質量を$m$、ばね定数を$k$として以下の問いに答えよ。

(1) 運動方程式を記述せよ。
(2) 物体の速度$v(t)$を求めよ。
(3) 物体の変位$x(t)$を求めよ。
(4) 物体の加速度$a(t)$を求めよ。
(5) $v(t), x(t), a(t)$のグラフを横軸$t$として描け。

解答

(1) 物体に作用する力は$x$軸において、ばねの復元力$kx$のみである。

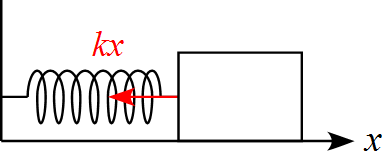
従って運動方程式は
\begin{align*}
ma=-kx
\end{align*}
となる。
(2) 運動方程式は
\begin{align*}
m\frac{\diff^2x}{\diff t^2}=-kx
\end{align*}
であるので、この一般解は
\begin{align*}
x&=\alpha\sin\omega t+\beta\cos\omega t\\
&=\sqrt{\alpha^2+\beta^2}\sin(\omega t+\delta)\\
&=A\sin(\omega t+\delta)\ , \quad \omega=\sqrt{\frac{k}{m}}
\end{align*}
である。

従って速度$v(t)$は
\begin{align*}
v(t)=\frac{\diff x}{\diff t}&=\frac{\diff}{\diff t}\Big[A\sin(\omega t+\delta)\Big]\\
&=A\omega\cos(\omega t+\delta)
\end{align*}
となる。

初期条件より$t=0$で$x=0,v=-v_0$より
\begin{align*}
x(0)=A\sin(\omega\cdot 0+\delta)&=0\\
\sin\delta&=0\\
\delta&=0
\end{align*}
\begin{align*}
v(t)=A\omega\cos(\omega\cdot 0+\delta)&=-v_0\\
A\omega\cos\delta&=-v_0\\
A\omega\cos\cdot 0&=-v_0\\
A\omega&=-v_0
\end{align*}
よって
\begin{align*}
v(t)=-v_0\cos\omega t=-v_0\cos\sqrt{\frac{k}{m}}t
\end{align*}
となる。
(3) 変位$x(t)$は
\begin{align*}
x(t)=A\sin\omega t&=-\frac{v_0}{\omega}\sin\omega t\\
&=-v_0\sqrt{\frac{m}{k}}\sin\sqrt{\frac{k}{m}}t
\end{align*}
となる。
(4) 加速度$a(t)$は
\begin{align*}
a(t)=\frac{\diff v}{\diff t}=\frac{\diff}{\diff t}(-v_0\cos\omega t)&=-v_0\cdot\sin\omega t\cdot(-\omega)\\
&=v_0\omega\sin\omega t\\
\\
&=v_0\sqrt{\frac{k}{m}}\sin\sqrt{\frac{k}{m}}t
\end{align*}
(5) 従って、それぞれのグラフは

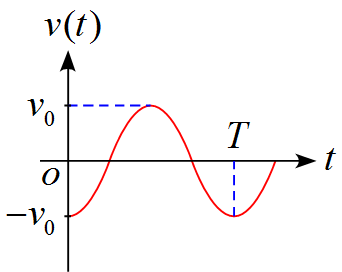
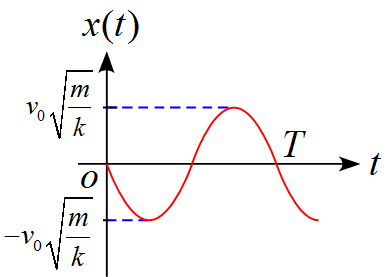
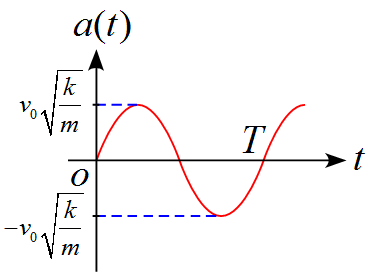
となる。