物体が滑り出さない条件

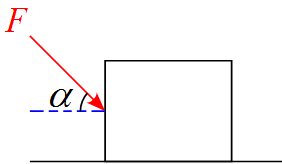
問題

粗い水平面上に置かれた質量$m$の物体に水平と$\alpha$の角をなす方向から
力$F$を加えたとする。物体が滑り出さないための力$F$の条件を求めよ。
但し、静止摩擦係数を$\mu$とする。

解答

$x,y$軸を設定し、物体に作用する力を書き込むと

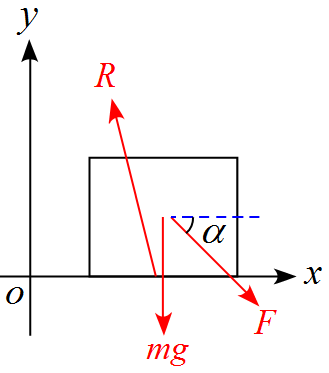
物体に作用する力は重力$mg$、抗力$R$、加える力$F$となる。
$x,y$軸に合わせて力を分解すると

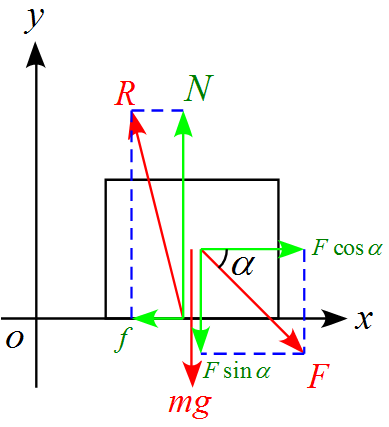
運動方程式は

$$\begin{align*} \begin{cases} ma_x=F\cos\alpha-f\\ ma_y=N-mg-F\sin\alpha \end{cases} \end{align*}$$
と表すことができる。

$a_y=0$より

$$\begin{align*} 0&=N-mg-F\sin\alpha\\ N&=mg+F\sin\alpha \end{align*}$$
となる。

物体が動き出さないためには$x$軸において

$$\begin{align*} F\cos\alpha-f<0 \end{align*}$$ のときである。

$f=\mu N$より

$$\begin{align*} F\cos\alpha-\mu(mg+F\sin\alpha)&<0\\ F\cos\alpha-\mu mg-\mu F\sin\alpha&<0\\ F(\cos\alpha-\mu \sin\alpha)-\mu mg&<0\\ -F(\mu \sin\alpha-\cos\alpha)-\mu mg&<0\\ F(\mu \sin\alpha-\cos\alpha)+\mu mg&>0 \end{align*}$$

ここで$\mu mg>0$であるため、$F$の係数である$\mu\sin\alpha-\cos\alpha$が正であれば、
$F$の大きさによらず滑り出さない。

即ち

$$\begin{align*} \mu\sin\alpha-\cos\alpha&>0\\ \tan\alpha&>\frac{1}{\mu} \end{align*}$$
が条件となる。

$$\begin{align*} \tan\alpha<\frac{1}{\mu} \end{align*}$$ の場合は$F$の大きさを考える必要があり、 $$\begin{align*} F(\cos\alpha-\mu\sin\alpha)-\mu mg&<0\\ F(\cos\alpha-\mu\sin\alpha)&<\mu mg\\ \\ F&<\frac{\mu mg}{\cos\alpha-\mu\sin\alpha} \end{align*}$$ であれば滑り出さないことになる。