球の表面に一様に帯電した球が作る電場

問題

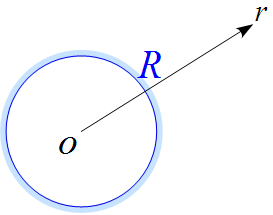
一様な面密度$\sigma$で球表面に帯電した半径$R$の球がある。以下の問いに答えよ。

(1) この球の中心からの距離$r \ (\ge R)$での電場の大きさ$E(r)$を求めよ。

(2) この球の中心からの距離$r \ (\le R)$での電場の大きさ$E(r)$を求めよ。

(3) 球の内外につくる静電場を距離$r$の関数としてグラフを書け。

解答

(1)
$r \ (\ge R)$の場合、ガウスの法則を適用する閉曲面を図のように半径$r$の球(赤の点線)を想定する。

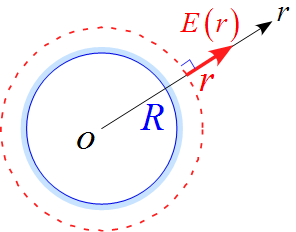
このとき、閉曲面内の電気量$Q$は

\begin{eqnarray*}
Q &=& \int_S \sigma \diff S\\
\\
&=& 4\pi R^2 \sigma
\end{eqnarray*}

である。

よって、この円筒(閉曲面)に対するガウスの法則は

\begin{eqnarray*}
\int_S \vec{E}\cdot \vec{n} ds &=& \frac{Q}{\varepsilon_0} \\
\\
E(r) 4\pi r^2 &=& \frac{1}{\varepsilon_0} 4\pi R^2 \sigma \\
\\
E(r) &=& \frac{\sigma}{\varepsilon_0} \frac{R^2}{r^2}
\end{eqnarray*}

となる。

(2)
$r \ (\le R)$の場合、ガウスの法則を適用する閉曲面を図のように半径$r$の球(赤の点線)を想定する。

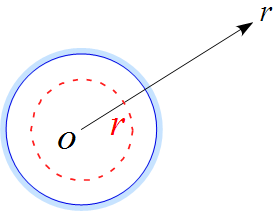
このとき、閉曲面内の電気量$Q$は

\begin{eqnarray*}
Q &=& \int_S \sigma \diff S\\
\\
&=& 0
\end{eqnarray*}

である。(球内部には電荷は無い)

よって、この円筒(閉曲面)に対するガウスの法則は

\begin{eqnarray*}
\int_S \vec{E}\cdot \vec{n} ds &=& \frac{Q}{\varepsilon_0}\\
\\
E(r) 4\pi r^2 &=& \frac{1}{\varepsilon_0} \cdot 0 \\
\\
E(r) &=& 0
\end{eqnarray*}

となる。

(3)
(1),(2)を$r$の関数としてグラフにすると

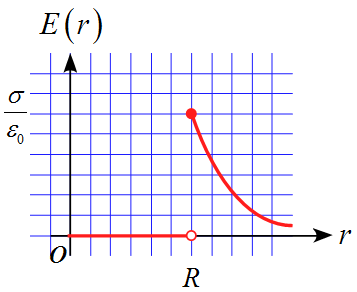
となる。
球内部には電場が生じないので、球表面までは$E(r)=0$となり、球表面に達した瞬間に$E(r) =\displaystyle \frac{\sigma}{\varepsilon_0} \frac{R^2}{r^2}$となる。