問題
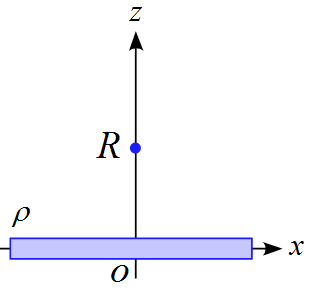
単位長さあたりの電気量(線密度)が$\rho$である無限に長い直線上に電荷が分布している。
以下の方法を用いて直線から距離$R$の位置での電場を求めよ。但し、線の太さは無視できるものとする。
(1) クーロンの法則を用いて電場を求めよ。
(2) ガウスの法則を用いて電場を求めよ。
解答
(1)
クーロンの法則を適用するために、直線の一部を微小部分$\diff x$を設定する。この微小部分$\diff x$が作る電場を計算し、全区間に対して積分を行うとする。
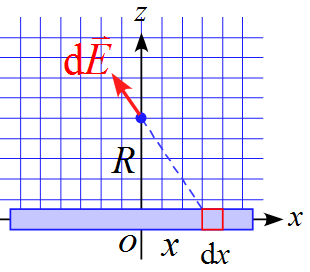
微小部分$\diff x$の電気量$\diff Q$は
\begin{eqnarray*}
\diff Q=\rho \diff x
\end{eqnarray*}
である。
よって微小部分$\diff x$が作る電場$\diff E$は
\begin{eqnarray*}
\diff E &=& \frac{1}{4\pi \varepsilon_0} \frac{\rho \diff x}{(\sqrt{R^2+x^2})^2} \\
\\
&=& \frac{1}{4\pi \varepsilon_0} \frac{\rho \diff x}{R^2+x^2}
\end{eqnarray*}
となる。
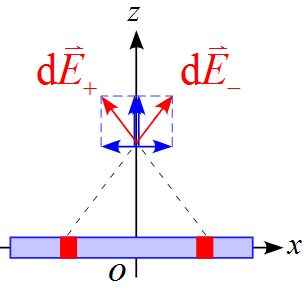
ここで、$\diff \vec{E}$の$x$成分は対称性により打ち消し合うので$z$成分だけ計算を行うと、
$z$成分の電場は
\begin{eqnarray*}
\diff E_z &=& \diff E \cos \theta \\
\\
&=& \frac{1}{4\pi \varepsilon_0} \frac{\rho \diff x}{r^2} \cdot \cos \theta \\
\end{eqnarray*}
となる。
これを全区間に対して積分を行うと、
\begin{eqnarray*}
E_z = \int_{-\infty}^{\infty} \diff E_z &=& \int_{-\infty}^{\infty} \frac{1}{4\pi \varepsilon_0} \frac{\rho \diff x}{r^2} \cdot \cos \theta \\
\end{eqnarray*}
となる。
上式は変数が$x, \ \theta$と混在しているので変数を$\theta$で統一する。
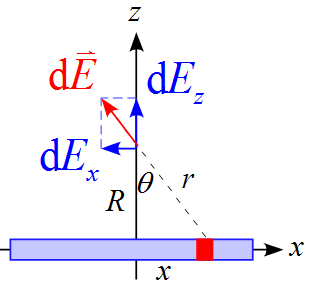
\begin{eqnarray*}
r &=& \frac{R}{\cos \theta} \\
\\
x &=& R \tan \theta \\
\\
\frac{\diff x}{\diff \theta} &=& R \frac{1}{\cos^2 \theta}
\end{eqnarray*}
積分区間は
\begin{eqnarray*}
x & : & -\infty \to + \infty \\
\\
\theta & : & -\frac{\pi}{2} \to + \frac{\pi}{2}
\end{eqnarray*}
である。
よって
\begin{eqnarray*}
E_z &=& \int_{-\infty}^{\infty} \frac{1}{4\pi \varepsilon_0} \frac{\rho \diff x}{r^2} \cdot \cos \theta \\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{4\pi \varepsilon_0} \frac{\rho \frac{R}{\cos^2 \theta}\diff \theta}{\left( \frac{R}{\cos \theta} \right)^2} \cos \theta \\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{4\pi \varepsilon_0} \frac{\rho}{R}\cos \theta \diff \theta \\
\\
&=& \frac{\rho}{4 \pi \varepsilon_0 R} \int _{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \theta \diff \theta \\
\\
&=& \frac{\rho}{4 \pi \varepsilon_0 R} [\sin \theta]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\
\\
&=& \frac{\rho}{4 \pi \varepsilon_0 R} \left[ \sin \left(\frac{\pi}{2} \right) - \sin \left(-\frac{\pi}{2} \right) \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\
\\
&=& \frac{\rho}{2 \pi \varepsilon_0 R}
\end{eqnarray*}
となる。
(2)
ガウスの法則を適用する閉曲面を図のように半径$R, \ $長さ$X$の円筒を想定する。
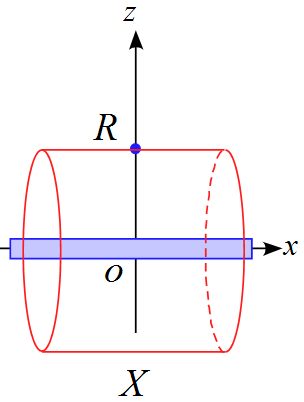
このとき、閉曲面内の電気量$Q$は
\begin{eqnarray*}
Q=\rho X
\end{eqnarray*}
である。
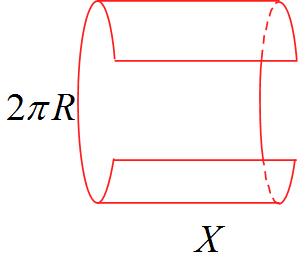
よって、この円筒(閉曲面)に対するガウスの法則は
\begin{eqnarray*}
\int_S \vec{E}\cdot \vec{n} ds &=& \frac{1}{\varepsilon_0} \int_l \rho dl \\
\\
E(z) 2\pi RX &=& \frac{1}{\varepsilon_0} \rho X \\
\\
E(z) &=& \frac{\rho}{2 \pi \varepsilon_0 R}
\end{eqnarray*}
となり、クーロンの法則を用いて求めた結果と一致する。