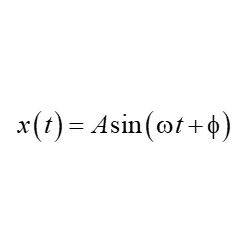鉛直ばね振り子
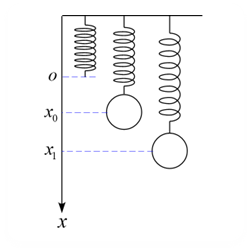
問題 軽いバネの一端を天井に固定して吊り下げた。このとき、バネの下端を原点とする。バネの下端に質量$m$の物体を取り付け、静止させた位置を$x_0$とする。物体をさらに$x_1$の位置まで引き下げ、静かに放して振動させた。物体を放した瞬間を$t=0$とする。以下の問いに答えよ。 (1) 物体の運動方程式を記述せよ。 (2) 物体の速度$v(t)$を求めよ。 (3) 物体の位置$x(t)$を求めよ。 解答 (1) 物体に作用する力は場の力「重力$mg$」と接触力「ばねの弾性力$kx$」なので運動方程式は \ ...
雨滴の落下
問題 質量$m$の雨滴が落下する運動を考える。このとき、速度に比例する空気抵抗が働き、その大きさを$kv$とする。以下の問いに答えよ。但し、初期条件$v(0)=0$とする。 (1) 運動方程式を記述せよ。 (2) 速度$v(t)$を求めよ。 (3) $v-t$グラフを描け。また原点での傾きを求めよ。 (4) 十分に時間が経過した状態の速度(終端速度)を求めよ。 解答 (1) 雨滴に作用する力は場の力「重力$mg$」と接触力「空気抵抗力$kv$」になります。 従って、運動方程式は \begin{eqnarr ...
単振動の平均エネルギー
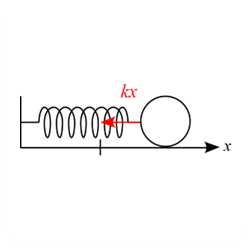
問題 質点が単振動している。1周期についての運動エネルギーの平均値$\bar{K}$と弾性力による位置エネルギーの平均値$\bar{U}$を求め、これらが等しいことを示せ。 解答 図のような単振動のモデルを考えた場合、 運動方程式は \begin{eqnarray*} m \frac{\diff v}{\diff t} =-kx \end{eqnarray*} となる。 両辺を$x$で積分すると、 \begin{eqnarray*} \int m\frac{\diff v}{\diff t}\diff x ...
単振り子の近似
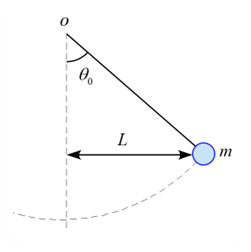
問題 質量$m$の物体が長さ$L$の糸で吊るされている。物体を鉛直線を基準に振れ角$\theta_0$で静かに手放した。この時の鉛直線からの距離を$A_0$とする。 以下の問いに答えよ。但し、振れ角$\theta_0$は十分に小さく、$A_0 \ll L$とする。 (1) 物体の運動方程式を記述せよ。 (2) 物体の運動を単振り子とみなしたとき、周期$T$、振幅$A$を求めよ。 (3) 物体を手放した時刻を$t=0$として、最下点を初めて通過する時刻$t_1$を求めよ。 (4) 物体の位置$x(t)$を$ ...
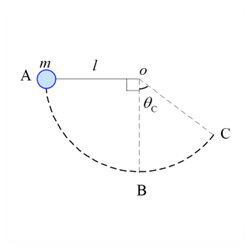
非等速円運動
問題 図のように、円の一部を軌道として運動するモデルを考える。 物体を糸の水平状態(点A)にして放し、円運動させ、点B(最下点)を通過し、点Cまで達した。運動中、糸は弛まず質量は無視できるほど軽いとする。 糸の長さ$l$、物体の質量$m$として以下の問いに答えよ。但し、重力加速度は$g$とする。 又、ある時刻$t$での糸と鉛直線のなす角を$\theta$として用いてよいとする。 (1) $r$方向、$\theta$方向の加速度を$a_r, a_\theta$としたとき、それぞれの方向の運動方程式を記述せよ ...
単振動の一般解から位置$x(t)$の決定
問題 単振動の一般解$x(t)=A \sin (\omega t + \phi)$において 以下の初期条件を満たすような関数$x(t)$を求めよ。 但し、$x_0, v_0$は定数とする。 (1) $x(0)=0 , \ v(0)=v_0$ (2) $x(0)=x_0 , \ v(0)=0$ (3) $x(0)=x_0 , \ v(0)=v_0$ (4) $x(t_1)=x_0 , \ v(t_1)=0$ 解答 単振動の一般解 \begin{eqnarray*} x(t)=A \sin (\omega t ...
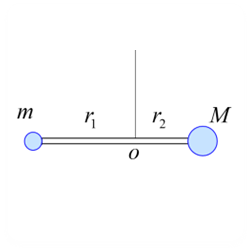
天秤が回転しない条件
問題 軽い棒の両端に質量$m$の物体と質量$M$の物体が図の様に取り付けられ、点$o$で糸に吊るされている。 この棒が回転しない条件を以下の問題に沿って答えよ。 (1) 棒に作用する力を書き込め。 (2) 棒の運動方程式を記述せよ。 (3) 棒の回転の運動方程式を記述せよ。 (4) 棒が回転しない条件$\displaystyle \frac{r_1}{r_2}$を求めよ。 解答 (1) 軸の設定は「$x$軸は右向き正」とし「$y$軸は上向き正」とします。 棒に作用する力は、左右の重り「重力$mg$」「重力 ...
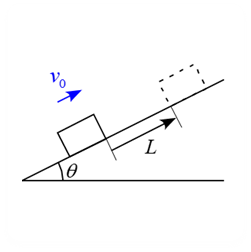
斜面を滑り上がる運動
問題 摩擦がある斜面を質量$m$の物体が滑り上がる運動を考える。 水平面となす角は$\theta$として以下の問いに答えよ。 但し、動摩擦力は$f=\mu_k N$として用いてよいとする。 斜面に沿って上向きに初速度$v_0$で物体を打ち出したところ、時刻$t_1$で移動距離$L$になり物体は止まった。 (1) この運動中に作用する力を書き込め。 (2) この運動の運動方程式を記述せよ。 (3) 運動方程式の両辺において距離積分を行い、仕事とエネルギーの関係式を導け。 (4) 動摩擦力がした仕事$W_{摩 ...
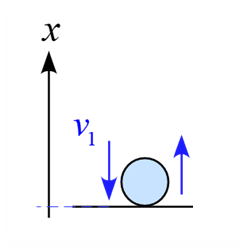
地表との衝突
問題 ある高さから質量$m$の物体を真下に投げ下ろしところ、地表に衝突する瞬間の速度の大きさが$v_1$となった。 (1) この衝突において力$F$が作用したとする。地表に衝突した瞬間の運動を記述せよ。 (2) この衝突において、力$F$は重力$mg$に比べて十分に大きく$F \gg mg$であり、又、衝突は完全弾性衝突であったとする。物体が地表から受けた力積$I$を運動方程式から導け。 解答 (1) 衝突した瞬間に作用する力は、場の力「重力 $mg$」と接触力「地表から受ける力$F$(抗力を含む)」なの ...
力学の問題を考える手順
運動学と力学の基本的な物理量の定義 運動学とは力学の分野の内で「物体の運動を時間や空間の観点から記述する学問」であり、力などの作用については言及しない分野です。 まずは力学の基本的な物理量である ・位置ベクトル $\vec{r}$ ・速度ベクトル $\vec{v}$ ・加速度ベクトル $\vec{a}$ の定義を確認しておきましょう。 速度ベクトル$\vec{v}$ 位置ベクトル$\vec{r}$を$\vec{r}=(x, y, z)$とすると 「速度ベクトル$\vec{v}$は位置ベクトル$\vec{r ...