問題
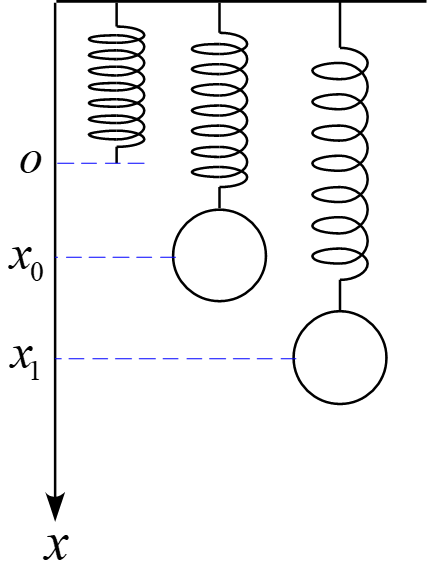
軽いバネの一端を天井に固定して吊り下げた。このとき、バネの下端を原点とする。バネの下端に質量$m$の物体を取り付け、静止させた位置を$x_0$とする。物体をさらに$x_1$の位置まで引き下げ、静かに放して振動させた。物体を放した瞬間を$t=0$とする。以下の問いに答えよ。
(1) 物体の運動方程式を記述せよ。
(2) 物体の速度$v(t)$を求めよ。
(3) 物体の位置$x(t)$を求めよ。
解答
(1)
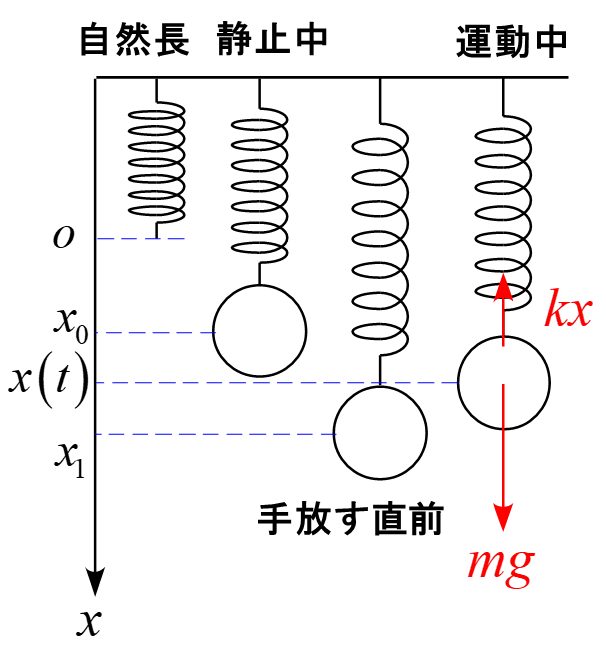
物体に作用する力は場の力「重力$mg$」と接触力「ばねの弾性力$kx$」なので運動方程式は
\begin{eqnarray*}
m a &=& mg-kx \\
\\
m \frac{\diff^2 x}{\diff t^2}&=& mg -kx
\end{eqnarray*}
となります。
(2), (3)
運動方程式をさらに式変形をすると、
\begin{eqnarray*}
m \frac{\diff^2 x}{\diff t^2}&=& -k \biggl( x- \frac{mg}{k} \biggr) \\
\end{eqnarray*}
となり、$\displaystyle X= x- \frac{mg}{k}$とおくと
\begin{eqnarray*}
\frac{\diff^2 X}{\diff t^2} &=& \frac{\diff}{\diff t} \biggl[ \frac{\diff}{\diff t} \biggl( x- \frac{mg}{k} \biggr) \biggr] \\
\\
&=& \frac{\diff}{\diff t} \biggl( \frac{\diff x}{\diff t} \biggr) \\
&=& \frac{\diff^2 x}{\diff t^2}
\end{eqnarray*}
であるから、運動方程式を書き換えると
\begin{eqnarray*}
m \frac{\diff^2 X}{\diff t^2}&=& = -k X \\
\end{eqnarray*}
となる。
この微分方程式の一般解は$\displaystyle \omega^2=\frac{k}{m}$とおくと
\begin{eqnarray*}
X(t) &=& A \sin (\omega t + \phi) \\
\end{eqnarray*}
と表され、$\displaystyle X= x- \frac{mg}{k}$より
\begin{eqnarray*}
x(t) - \frac{mg}{k}&=& A \sin (\omega t + \phi) \\
\\
x(t) &=& A \sin (\omega t + \phi) + \frac{mg}{k}\\
\end{eqnarray*}
となります。速度$v(t)$については
\begin{eqnarray*}
v(t) = \frac{\diff x(t)}{\diff t}
&=& \frac{\diff}{\diff t} \biggl[ A \sin (\omega t + \phi) + \frac{mg}{k}\ \biggr] \\
\\
&=& A \omega \cos (\omega t + \phi)
\end{eqnarray*}
となります。
初期条件$v(0)=0 , x(0)=x_1$より
\begin{eqnarray*}
v(0) = A \omega \cos (\omega \cdot 0 + \phi) &=& 0 \\
\\
A \omega \cos \phi &=& 0 \\
\\
\cos \phi &=& 0 \qquad (A\omega \ne 0) \\
\\
\phi = \frac{\pi}{2}
\end{eqnarray*}
となり、
\begin{eqnarray*}
x(0) = A \sin \biggl(\omega \cdot 0 + \frac{\pi}{2} \biggr) + \frac{mg}{k} &=& x_1 \\
\\
A \sin \frac{\pi}{2} + \frac{mg}{k} &=& x_1 \\
\\
A + \frac{mg}{k} &=& x_1 \\
\\
A &=& x_1 - \frac{mg}{k}
\end{eqnarray*}
となる。
ここで、位置$x_0$で静止させた場合の運動方程式は$a=0, x=x_0$より
\begin{eqnarray*}
0 &=& mg -kx_0 \\
\\
x_0 &=& \frac{mg}{k}
\end{eqnarray*}
と表される。
従って、位置$x(t)$については
\begin{eqnarray*}
x(t) &=& \biggl( x_1 - \frac{mg}{k} \biggr) \sin \biggl( \omega t + \frac{\pi}{2} \biggr) + \frac{mg}{k} \\
\\
&=& \bigl( x_1 - x_0 \bigr) \cos \omega t + \frac{mg}{k} \\
\\
&=& \bigl( x_1 - x_0 \bigr) \cos \sqrt{\frac{k}{m}} t + \frac{mg}{k}
\end{eqnarray*}
となり、速度$v(t)$については
\begin{eqnarray*}
v(t) &=& \biggl( x_1 - \frac{mg}{k} \biggr) \omega \cos \biggl( \omega t + \frac{\pi}{2} \biggr) \\
\\
&=& -\bigl( x_1 - x_0 \bigr) \omega \sin \omega t \\
\\
&=& \bigl( x_0 - x_1 \bigr) \omega \sin \omega t \\
\\
&=& \bigl( x_0 - x_1 \bigr) \sqrt{\frac{k}{m}} \cos \sqrt{\frac{k}{m}} t
\end{eqnarray*}
となる。