問題
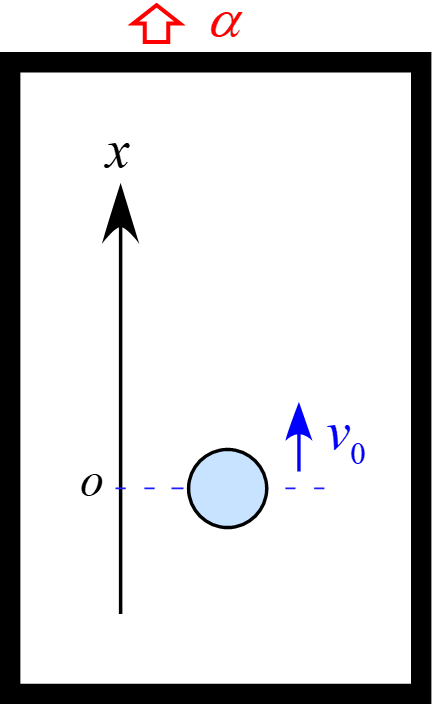
一定の加速度$\alpha$で上昇するエレベータがある。
このエレベータ内で、質量$m$の物体を初速度$v_0$で鉛直上方に投げ上げた。投げ上げた瞬間を$t=0$とし、その位置を原点とすると、時刻$t_1$に再び原点に戻ってきた。
以下の問いに答えよ。
(1) 物体の運動方程式を記述せよ。
(2) 物体の速度$v(t)$を求めよ。
(3) 物体の位置$x(t)$を求めよ。
(4) エレベーターの加速度$\alpha$を求めよ。
解答
(1)
座標軸をエレベータ内に上向き正に設定します。
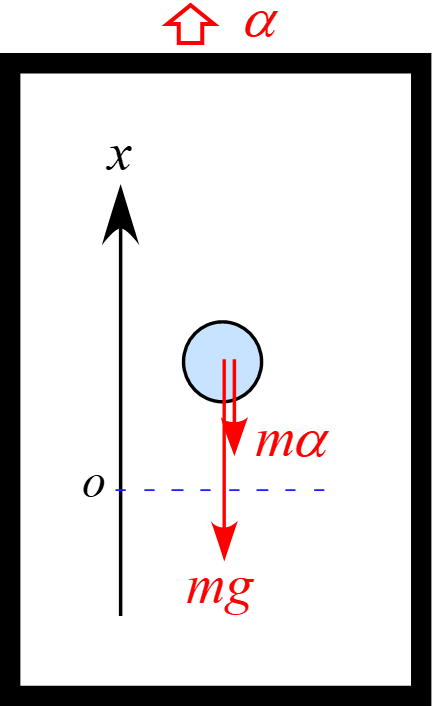
物体に作用する力は、場の力「重力$mg$」と慣性力「$m\alpha$」になります。
エレベータは上昇中なので、慣性力の向きはエレベータの進行方向と逆向きになります。
従って、
\begin{eqnarray*}
m a &=& -mg-m \alpha \\
\\
m \frac{\diff v}{\diff t}&=& -mg-m \alpha
\end{eqnarray*}
となります。
(2)
運動方程式より
\begin{eqnarray*}
\frac{\diff v}{\diff t}&=& -g- \alpha
\end{eqnarray*}
となる。両辺$t$で積分すると
\begin{eqnarray*}
\int \frac{\diff v}{\diff t} \diff t &=& \int (-g- \alpha ) \diff t \\
\\
\int \diff v &=& \int (-g- \alpha ) \diff t \\
\\
v &=& (-g- \alpha ) t +C_1 \qquad (C_1 : \mbox{積分定数})
\end{eqnarray*}
となる。初期条件$v(0)=v_0$より
\begin{eqnarray*}
v (0) = (-g- \alpha ) \cdot 0 +C_1 &=& v_0 \\
\\
C_1 &=& v_0 \\
\end{eqnarray*}
となるので、速度$v(t)$は
\begin{eqnarray*}
v (t) = -(g+ \alpha ) t + v_0 \\
\end{eqnarray*}
となる。
(3)
(2)の結果をさらに$t$で積分すると
\begin{eqnarray*}
v = \frac{\diff x}{\diff t} &=& -(g+ \alpha ) t + v_0 \\
\\
\int \frac{\diff x}{\diff t} \diff t &=& \int \bigl( -(g+ \alpha ) t + v_0 \bigr) \diff t \\
\\
\int \diff x &=& \int \bigl( -(g+ \alpha ) t + v_0 \bigr) \diff t \\
\\
x &=& - \frac{1}{2} (g+ \alpha ) t^2 + v_0 t +C_2 \qquad (C_2 : \mbox{積分定数})\\
\end{eqnarray*}
となる。初期条件$x(0)=0$より
\begin{eqnarray*}
x (0) = - \frac{1}{2} (g+ \alpha ) \cdot 0^2 + v_0 t +C_2 &=& 0 \\
\\
C_2 &=& 0 \\
\end{eqnarray*}
となるので、位置$x(t)$は
\begin{eqnarray*}
x (t) = -\frac{1}{2} (g + \alpha ) t^2 + v_0 t \\
\end{eqnarray*}
となる。
(4)
$t=t_1$のとき、再び戻って来るので位置$x(t_1)$は
\begin{eqnarray*}
x (t_1) = -\frac{1}{2} (g + \alpha ) t_1^2 + v_0 t_1 &=& 0 \\
\\
t_1 \biggl( -\frac{1}{2} (g + \alpha ) t_1 + v_0 \biggr) &=& 0
\end{eqnarray*}
となり、$t_1=0$なので
\begin{eqnarray*}
-\frac{1}{2} (g + \alpha ) t_1 + v_0 &=& 0 \\
\\
\frac{1}{2} (g + \alpha ) t_1 &=& v_0 \\
\\
g + \alpha &=& v_0 \ \frac{2}{t_1} \\
\\
\alpha &=& \frac{2v_0}{t_1} -g \\
\end{eqnarray*}
となる。