斜面を滑らない条件

問題

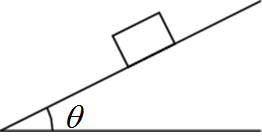
水平と角度 $\theta$ をなす荒い斜面上に置かれた物体が滑り出さないための条件を求めよ。
但し、静止摩擦係数を $\mu$ とする。

解答

まずは作図をする。

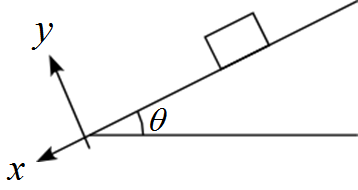
この運動は2次元的に動くので
2つの軸を設定する必要がある。
そこで、斜面に平行な軸を$x$とし
斜面に垂直な軸を$y$とする。

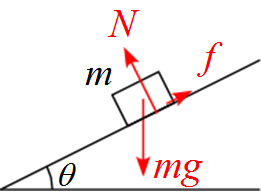
物体に作用する力を書き込むと、物体の質量を$m$として、

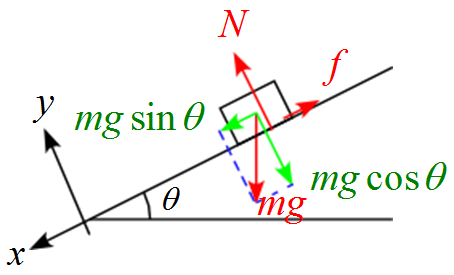
$x$,$y$軸に合わせて力を分解すると

物体が静止している時、
運動方程式はそれぞれの加速度を$a_x$, $a_y$として
\begin{align*}
\begin{cases}
ma_x=mg\sin\theta-f&\\
ma_y=N-mg\cos\theta&
\end{cases}
\end{align*}
と表すことができる。
静止しているので、$a_x=0$, $a_y=0$より
\begin{align*}
\begin{cases}
0=mg\sin\theta-f&\\
0=N-mg\cos\theta&
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
f = mg\sin\theta&\\
N = mg\cos\theta&
\end{cases}
\end{align*}
となる。
$\theta$が大きくなると、それに応じて$f$も大きくならないと
静止していられなくなる。
しかし、摩擦力$f$は限界があり、最大で$\mu$$N$である。
\begin{align*}
f_{\rm max}=\mu N
\end{align*}
となる。
よって滑り出す限界は
\begin{align*}
f_{\rm max}=mg \sin\theta&=\mu N\\
&= \mu mg\cos\theta_{\rm max}\\
\sin \theta_{\rm max}&=\mu\cos\theta_{\rm max}\\
\tan \theta_{\rm max}&=\mu
\end{align*}
である。
従って
\begin{align*}
\tan\theta&<\mu \end{align*} であれば滑り出さないことになる。