問題
質量$m$の雨滴が落下する運動を考える。このとき、速度に比例する空気抵抗が働き、その大きさを$kv$とする。以下の問いに答えよ。但し、初期条件$v(0)=0$とする。
(1) 運動方程式を記述せよ。
(2) 速度$v(t)$を求めよ。
(3) $v-t$グラフを描け。また原点での傾きを求めよ。
(4) 十分に時間が経過した状態の速度(終端速度)を求めよ。
解答
(1)
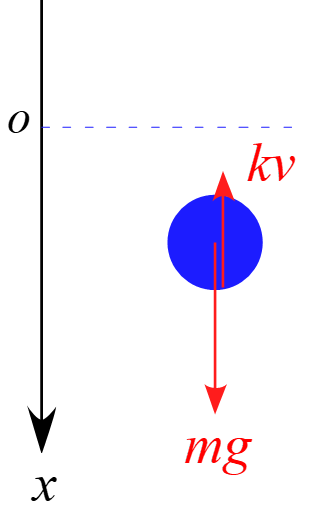
雨滴に作用する力は場の力「重力$mg$」と接触力「空気抵抗力$kv$」になります。
従って、運動方程式は
\begin{eqnarray*}
m a =mg -kv
\end{eqnarray*}
となります。
(2)
運動方程式は
\begin{eqnarray*}
m \frac{\diff v}{\diff t} &=& mg -kv \\
\\
\frac{\diff v}{\diff t} &=& g - \frac{k}{m} v
\end{eqnarray*}
となり、変数分離の形で解く微分方程式になります。
\begin{eqnarray*}
\frac{\diff v}{\diff t} &=& - \frac{k}{m} v + g \\
\\
\frac{\diff v}{\diff t} &=& - \frac{k}{m} \biggl(v - g \cdot \frac{m}{k} \biggr) \\
\\
\frac{\diff v}{\diff t} &=& - \frac{k}{m} \biggl(v - \frac{mg}{k} \biggr) \\
\\
\frac{\diff v}{v - \frac{mg}{k}} &=& - \frac{k}{m} \diff t \\
\end{eqnarray*}
となり、両辺積分すると
\begin{eqnarray*}
\int \frac{\diff v}{v - \frac{mg}{k}} &=& \int \biggl(- \frac{k}{m} \biggr) \diff t \\
\\
\log \bigl| v - \frac{mg}{k} \bigr| &=& - \frac{k}{m} t +C_1 \\
\\
\bigl| v - \frac{mg}{k} \bigr| &=& e^{- \frac{k}{m} t +C_1} \\
\\
\bigl| v - \frac{mg}{k} \bigr| &=& e^{C_1} e^{- \frac{k}{m} t} \\
\\
\bigl| v - \frac{mg}{k} \bigr| &=& C_2 e^{- \frac{k}{m} t} \\
\\
v - \frac{mg}{k} &=& C_2 e^{- \frac{k}{m} t} \\
\\
v &=& C_2 e^{- \frac{k}{m} t} + \frac{mg}{k} \\
\end{eqnarray*}
となります。初期条件$v(0)=0$より
\begin{eqnarray*}
v(0) = C_2 e^{- \frac{k}{m} \cdot 0} + \frac{mg}{k} &=& 0 \\
\\
C_2 + \frac{mg}{k} &=& 0 \\
\\
C_2 &=& - \frac{mg}{k} \\
\end{eqnarray*}
となるので、速度$v(t)$は
\begin{eqnarray*}
v(t) &=& - \frac{mg}{k} e^{- \frac{k}{m}t} + \frac{mg}{k} \\
\\
v(t) &=& \frac{mg}{k} \biggl(1- e^{- \frac{k}{m}t} \biggr)
\end{eqnarray*}
となります。
(3)
$v-t$グラフの傾きとなる加速度$a(t)$について考えると、
\begin{eqnarray*}
a(t) = \frac{\diff}{\diff t} [v(t)] &=& \frac{\diff}{\diff t} \biggl[ \frac{mg}{k} \biggl(1- e^{- \frac{k}{m}t} \biggr) \biggr] \\\\
&=& \frac{mg}{k} \biggl[ \biggl(1- e^{- \frac{k}{m}t} \biggr) \biggr] \\
\\
&=& \frac{mg}{k} \cdot - e^{- \frac{k}{m}t} \cdot - \frac{k}{m} \\
\\
&=& ge^{- \frac{k}{m}t}
\end{eqnarray*}
となる。
$t=0$のとき、
\begin{eqnarray*}
a(0) &=& g\cdot e^{- \frac{k}{m} \cdot 0} =g
\end{eqnarray*}
となり、$t=\infty$のとき
\begin{eqnarray*}
a(\infty) &=& g\cdot e^{- \frac{k}{m} \cdot \infty} =0
\end{eqnarray*}
となる。
速度$v(t)$については
$t=0$のとき、
\begin{eqnarray*}
v(0) &=& \frac{mg}{k} \biggl(1- e^{- \frac{k}{m} \cdot 0} \biggr) =0
\end{eqnarray*}
となり、$t=\infty$のとき
\begin{eqnarray*}
v(\infty) &=& \frac{mg}{k} \biggl(1- e^{- \frac{k}{m} \cdot \infty} \biggr) = \frac{mg}{k}
\end{eqnarray*}
となる。
以上より$v-t$グラフは
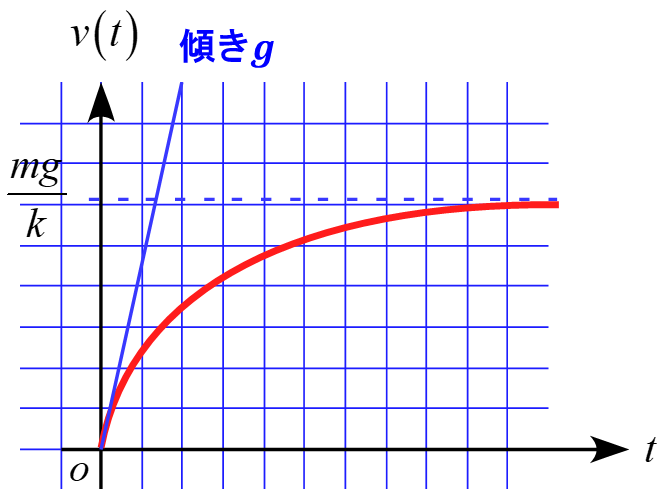
となる
(4)
(3)の結果より
\begin{eqnarray*}
v(\infty) &=& \frac{mg}{k}
\end{eqnarray*}
が終端速度となる。
$\displaystyle v - \frac{mg}{k}$が負の場合
上で計算した場合は$\displaystyle v - \frac{mg}{k}$を正として計算していましたが、負の場合も確認しておきましょう。
\begin{eqnarray*}
- \biggl( v - \frac{mg}{k} \biggr) &=& C_2 e^{- \frac{k}{m} t} \\
\\
- v + \frac{mg}{k} &=& C_2 e^{- \frac{k}{m} t} \\
\\
v &=& -C_2 e^{- \frac{k}{m} t} + \frac{mg}{k} \\
\end{eqnarray*}
となり、初期条件$v(0)=0$より
\begin{eqnarray*}
v(0) = -C_2 e^{- \frac{k}{m} \cdot 0} + \frac{mg}{k} &=& 0 \\
\\
-C_2 + \frac{mg}{k} &=& 0
\\
C_2 &=& \frac{mg}{k}
\end{eqnarray*}
従って、速度$v(t)$は
\begin{eqnarray*}
v(t) &=& - \frac{mg}{k} e^{- \frac{k}{m}t} + \frac{mg}{k} \\
\\
v(t) &=& \frac{mg}{k} \biggl(1- e^{- \frac{k}{m}t} \biggr)
\end{eqnarray*}
となるので、同じ結果となります。