問題
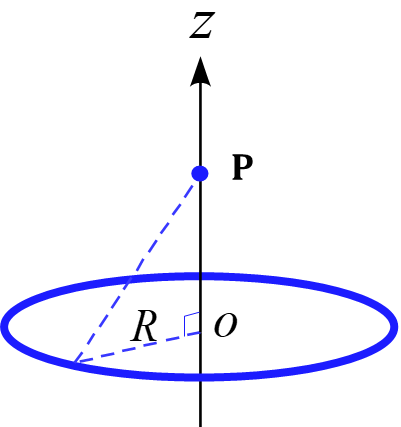
図のような$z$軸を中心軸に持つ半径$R$のリング状に線密度$\rho$で電荷が一様に分布している。
線の太さは無視できるものとして、以下の問いに答えよ。
(1) OPの距離を$z$とすると、点Pでの電場の大きさを求めよ。
(2) OPの距離を$z$とすると、点Pでの電位の大きさを求めよ。
但し、電位の基準は無限遠とする。
解答
(1)
クーロンの法則を適用するために、リングの一部を微小部分$\diff s$と設定する。この微小部分$\diff s$が作る電場$\diff E$を計算し、全区間に対して積分を行うとする。
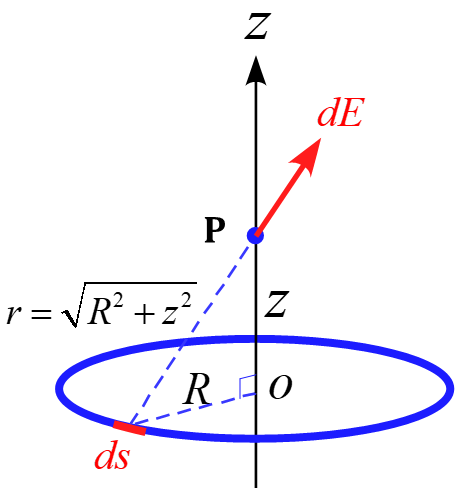
微小部分$\diff s$の長さは、微小部分のなす角を$\diff \phi$とすると、$R \diff \phi$と表されるので、微小部分$\diff s$の電荷$\diff Q$は
\begin{eqnarray*}
\diff Q =\rho R \diff \phi
\end{eqnarray*}
である。
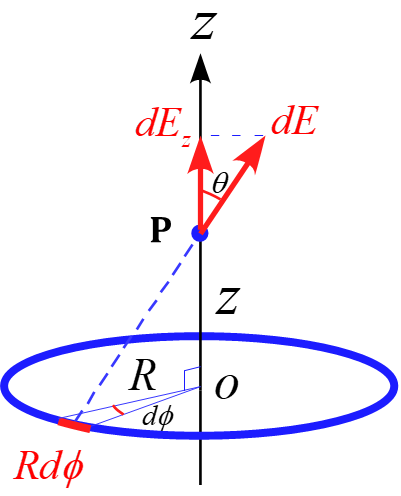
従って、この微小部分$\diff s$が点Pで作る電場$\diff E$は微小部分から点Pまでの距離を$r$とすると
\begin{eqnarray*}
\diff E=\frac{1}{4\pi \varepsilon_0}\frac{\rho R \diff \phi}{r^2}
\end{eqnarray*}
と表される。
この微小部分は、円の反対側にも同様の微小部分を考えることができるので、対称性により、$z$成分のみ計算すれはよい。
微小部分が作る電場の$z$成分$\diff E_z$は$\diff E$と$\diff E_z$のなす角を$\theta$とすると、
\begin{eqnarray*}
\diff E_z =\diff E \ \cos \theta
\end{eqnarray*}
であるから、
\begin{eqnarray*}
\diff E_z =\frac{1}{4\pi \varepsilon_0}\frac{\rho R \diff \phi}{r^2} \ \cos \theta
\end{eqnarray*}
と表される。
ここで、$\diff E$と$\diff E_z$のなす角$\theta$について
\begin{eqnarray*}
\cos \theta=\frac{z}{r}
\end{eqnarray*}
の関係であるから
\begin{eqnarray*}
\diff E_z &=&\frac{1}{4\pi \varepsilon_0}\frac{\rho R \diff \phi}{r^2} \ \frac{z}{r}\\
\\
&=& \frac{1}{4\pi \varepsilon_0}\frac{\rho R z}{r^3} \ \diff \phi
\end{eqnarray*}
となる。
従って、全電場$E_z$は
\begin{eqnarray*}
E_z &=&\frac{1}{4\pi \varepsilon_0}\frac{\rho R z}{r^3} \ \displaystyle \int_{0}^{2\pi} \diff \phi \\
\\
&=& \frac{1}{4\pi \varepsilon_0} \frac{\rho R z}{r^3} \cdot 2\pi \\
\\
&=& \frac{\rho Rz}{2 \varepsilon_0 (R^2 + z^2)^{\frac{3}{2}}}
\end{eqnarray*}
となる。
(2)
電位$V$についても電場$E$と同様に微小部分を考えると、微小部分による電位$\diff V$は
\begin{eqnarray*}
\diff V =\frac{1}{4\pi \varepsilon_0}\frac{\rho R \diff \phi}{r}
\end{eqnarray*}
である。
従って、電位$V$は
\begin{eqnarray*}
V &=& \frac{1}{4\pi \varepsilon_0}\frac{\rho R }{r} \int_{0}^{2\pi
}\diff \phi\\
\\
&=& \frac{1}{4\pi \varepsilon_0}\frac{\rho R }{r} \cdot 2\pi \\
\\
&=& \frac{\rho R}{2 \varepsilon_0 r} \\
\\
&=& \frac{\rho R}{2 \varepsilon_0 \sqrt{R^2+z^2}} \\
\end{eqnarray*}
となる。
別解
電場と電位の関係
\begin{eqnarray*}
E_z =- \frac{\partial V}{\partial z}
\end{eqnarray*}
を利用して、(2)から先に計算して、(1)を求めても良い。
従って、電場$E_z$は
\begin{eqnarray*}
E_z &=& - \frac{\partial V}{\partial z} \\
\\
&=& - \frac{\partial}{\partial z} \biggl[\frac{\rho R}{2 \varepsilon_0 \sqrt{R^2+z^2}}\biggr] \\
\\
&=& -\frac{\rho R}{2 \varepsilon_0} \frac{\partial}{\partial z} \biggl[\frac{1}{{(R^2+z^2)}^{\frac{1}{2}}}\biggr] \\
\\
&=& -\frac{\rho R}{2 \varepsilon_0} \frac{\partial}{\partial z} [(R^2+z^2)^{-\frac{1}{2}}] \\
\\
&=& -\frac{\rho R}{2 \varepsilon_0} \cdot \ - \frac{1}{2} (R^2+z^2)^{-\frac{3}{2}} \cdot 2z \\
\\
&=& \frac{\rho R z}{2 \varepsilon_0} (R^2+Z^2)^{-\frac{3}{2}} \\
\\
&~& \frac{\rho Rz}{2 \varepsilon_0 (R^2 + Z^2)^{\frac{3}{2}}}
\end{eqnarray*}
となり、(1)と同じ結果を得る。