2次元平面の極座標表示における速度$\vec{v}=(v_r, v_\theta)$及び加速度$\vec{a}=(a_r, a_\theta)$を単位ベクトルを使って導出する
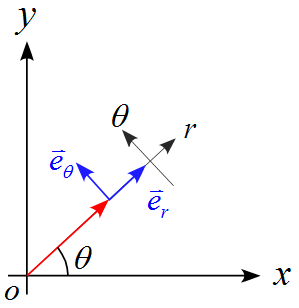
速度・加速度の極座標表示
運動の軌道の種類によっては極座標で扱った方が理解しやすいことも多い。
ここでは、2次元平面における極座標表示について単位ベクトルを用いて導出する。。
2次元平面の極座標
図のように、位置ベクトル$\vec{r}$と$x$軸とのなす角を$\theta$とする。
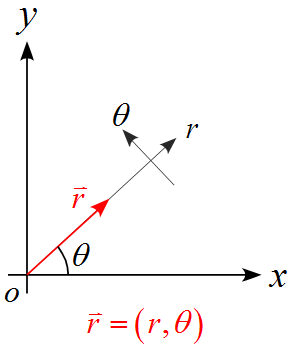
2次元平面の極座標の速度
位置ベクトル$\vec{r}$は極座標の単位ベクトルを用いて表すと
\begin{eqnarray*}
\vec{r} = r \vec{e}_r
\end{eqnarray*}
と表される。
従って、速度ベクトル$\vec{v}$は極座標の単位ベクトルを用いて表すと
\begin{eqnarray*}
\vec{v} = \frac{\diff \vec{r}}{\diff t} &=& \frac{\diff}{\diff t} ( r \vec{e}_r ) \\
\\
&=& \frac{\diff r}{dt} \vec{e}_r + r \frac{\diff \vec{e}_r}{\diff t}
\end{eqnarray*}
となる。
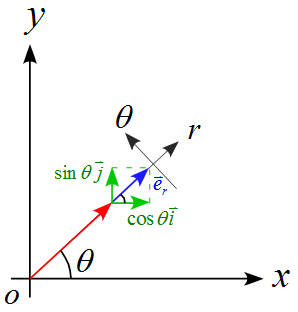
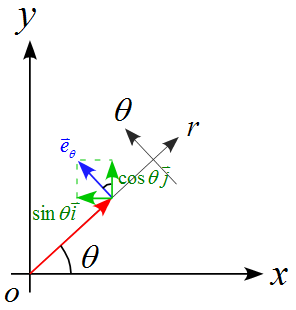
ここで、極座標の単位ベクトル$\vec{e}_r , \vec{e}_\theta$を$x,y$軸に分解すると下図より
\begin{eqnarray*}
\vec{e}_r =
\begin{pmatrix}
\cos \theta \\
\sin \theta \\
\end{pmatrix}
\ \ \ \
\vec{e}_\theta =
\begin{pmatrix}
-\sin \theta \\
\cos \theta \\
\end{pmatrix}
\end{eqnarray*}
であるから、
\begin{eqnarray*}
\frac{\diff}{\diff t}\left[ \vec{e}_r \right] &=&
\begin{bmatrix}
\frac{\diff}{\diff t} (\cos \theta) \\
\frac{\diff}{\diff t} (\sin \theta) \\
\end{bmatrix}
=
\begin{bmatrix}
-\sin \theta \frac{\diff \theta}{\diff t} \\
\cos \theta \frac{\diff \theta}{\diff t} \\
\end{bmatrix}
= \frac{\diff \theta}{\diff t}
\begin{pmatrix}
-\sin \theta \\
\cos \theta \\
\end{pmatrix}
= \frac{\diff \theta}{\diff t} \vec{e}_\theta
\\ \\
\frac{\diff}{\diff t}\left[ \vec{e}_\theta \right] &=&
\begin{bmatrix}
\frac{\diff}{\diff t} (-\sin \theta) \\
\frac{\diff}{\diff t} ( \cos \theta) \\
\end{bmatrix}
=
\begin{bmatrix}
-\cos \theta \frac{\diff \theta}{\diff t} \\
-\sin \theta \frac{\diff \theta}{\diff t} \\
\end{bmatrix}
= -\frac{\diff \theta}{\diff t}
\begin{pmatrix}
\cos \theta \\
\sin \theta \\
\end{pmatrix}
= -\frac{\diff \theta}{\diff t} \vec{e}_r
\end{eqnarray*}
となる。
従って、前式の速度$\vec{v}$は
\begin{eqnarray*}
\vec{v} &=& \frac{\diff r}{dt} \vec{e}_r + r \frac{\diff \vec{e}_r}{\diff t} \\
\\
&=& \frac{\diff r}{dt} \vec{e}_r + r \cdot \frac{\diff \theta}{dt} \vec{e}_\theta
\end{eqnarray*}
と表され、
\begin{eqnarray*}
v_r = \frac{\diff r}{dt} , \ v_\theta = r \frac{\diff \theta}{dt}
\end{eqnarray*}
となる。
2次元平面の極座標の加速度
さらに、加速度$\vec{a}$は
\begin{eqnarray*}
\vec{a} = \frac{\diff \vec{v}}{\diff t} &=& \frac{\diff}{\diff t} ( v_r \vec{e}_r + v_\theta \vec{e}_\theta ) \\
\\
&=& \frac{\diff v_r}{\diff t}\vec{e}_r + v_r \frac{\diff \vec{e}_r}{\diff t} + \frac{\diff v_\theta}{\diff t}\vec{e}_\theta + v_\theta \frac{\diff \vec{v}_\theta}{\diff t}\\
\\
&=& \frac{\diff}{\diff t} \left( \frac{\diff r}{\diff t} \right) \vec{e}_r +
\frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t} \vec{e}_\theta +
\frac{\diff}{\diff t} \left( r \frac{\diff \theta}{\diff t} \right) \vec{e}_\theta +
r \frac{\diff \theta}{\diff t} \left( - \frac{\diff \theta}{\diff t} \right) \vec{e}_r \\
\\
&=& \frac{\diff ^2 r}{\diff t^2} \vec{e}_r + \frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t} \vec{e}_\theta +
\left[ \frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t}
+ r \frac{\diff}{\diff t} \left( \frac{\diff \theta}{\diff t} \right) \right] \vec{e}_\theta
- r \left( \frac{\diff \theta}{\diff t} \right) ^2 \vec{e}_r \\
\\
&=& \left[ \frac{\diff ^2 r}{\diff t^2} - r \left( \frac{\diff \theta}{\diff t} \right) ^2\right] \vec{e}_r +
\left[ 2 \frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t} + r \frac{\diff ^2 \theta}{\diff t^2} \right] \vec{e}_\theta
\\
\end{eqnarray*}
と表され、
\begin{eqnarray*}
a_r &=& \frac{\diff ^2 r}{\diff t^2} - r \left( \frac{\diff \theta}{\diff t} \right) ^2 \\
\\
a_\theta &=& 2 \frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t} + r \frac{\diff ^2 \theta}{\diff t^2}
\end{eqnarray*}
となる。