問題
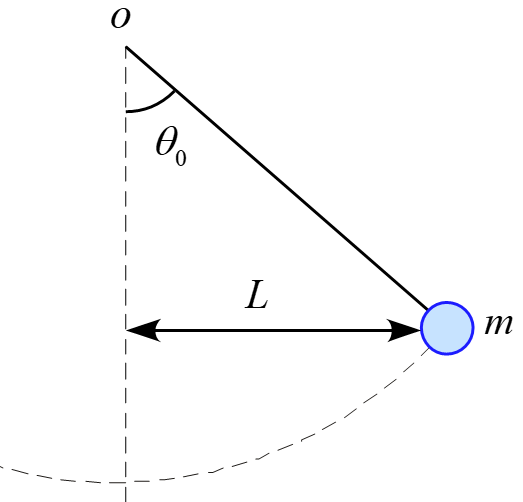
質量$m$の物体が長さ$L$の糸で吊るされている。物体を鉛直線を基準に振れ角$\theta_0$で静かに手放した。この時の鉛直線からの距離を$A_0$とする。
以下の問いに答えよ。但し、振れ角$\theta_0$は十分に小さく、$A_0 \ll L$とする。
(1) 物体の運動方程式を記述せよ。
(2) 物体の運動を単振り子とみなしたとき、周期$T$、振幅$A$を求めよ。
(3) 物体を手放した時刻を$t=0$として、最下点を初めて通過する時刻$t_1$を求めよ。
(4) 物体の位置$x(t)$を$x(t)-t$グラフとして描け。
解答
(1)
運動中、物体に作用する力は場の力の「重力$mg$」と接触力の「糸の張力$S$」になります。
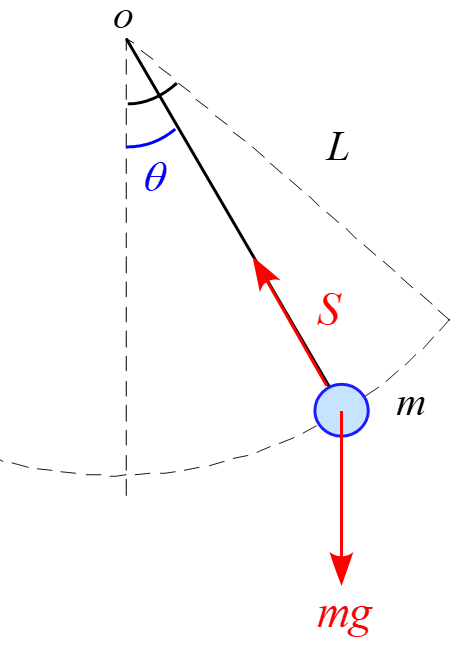
極座標$r , \theta$を設定し、軸に沿って分解すると図のようになります。
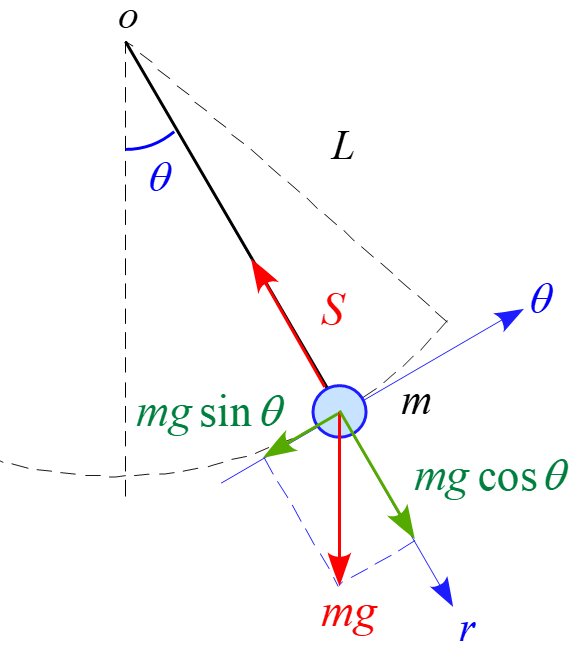
従って、運動方程式は
\begin{eqnarray*}
ma_r &=& mg \cos \theta -S \\
\\
ma_\theta &=& -mg \sin \theta
\end{eqnarray*}
と表されます。
(2)

ある時刻$t$での鉛直線からの距離を$x$とすると図の位置関係より
\begin{eqnarray*}
\sin \theta = \frac{x}{L}
\end{eqnarray*}
であり、加速度については、極座標と直交座標の関係と$x< A_0 \ll L$より
\begin{eqnarray*}
\cos \theta = \frac{L}{\sqrt{L^2-x^2}}
= \frac{L}{\sqrt{L^2 \biggl[ 1- \biggl(\frac{x}{L}\biggr)^2 \biggr]}} \simeq 1
\end{eqnarray*}
となるので、
\begin{eqnarray*}
a_x = a_\theta \cos \theta \simeq a_\theta
\end{eqnarray*}
と表されます。
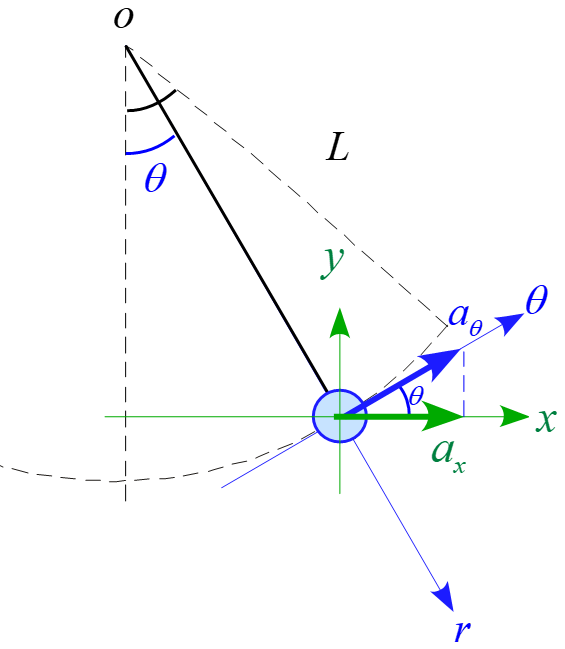
従って、$\theta$方向の運動方程式は
\begin{eqnarray*}
ma_x \simeq -mg \sin \theta = -mg \frac{x}{L}
\end{eqnarray*}
と書き換えられます。
よって、位置$x$は
\begin{eqnarray*}
\frac{\diff^2 x}{\diff t^2} = - \frac{g}{L} x
\end{eqnarray*}
で表される微分方程式になります。
この微分方程式の一般解は
\begin{eqnarray*}
x(t) =A \sin (\omega t + \phi)
\end{eqnarray*}
で表されるので($\displaystyle \omega = \sqrt{\frac{g}{L}}$)、速度$v(t)$は
\begin{eqnarray*}
v(t) =A \omega \cos (\omega t + \phi)
\end{eqnarray*}
となります。
この式に初期条件$t=0$で$v(0)=0 , x(0)=A_0$を適用すると
\begin{eqnarray*}
v(0) =A \omega \cos (\omega \cdot 0 + \phi) &=& 0 \\
\\
A \omega \cos \phi &=& 0
\end{eqnarray*}
$A \ne 0 ,\omega \ne 0$なので
\begin{eqnarray*}
\cos \phi &=& 0 \\
\\
\phi &=& \frac{\pi}{2}
\end{eqnarray*}
一方、位置$x(t)$については$x(0)=A_0$より
\begin{eqnarray*}
x(0)=A \sin \bigl(\omega \cdot 0 + \frac{\pi}{2}\bigr) &=& A_0 \\
\\
A \sin \frac{\pi}{2} &=& A_0 \\
\\
A &=& A_0
\end{eqnarray*}
となる。
従って、位置$x(t)$の関数は
\begin{eqnarray*}
x(t) &=& A_0 \sin \bigl(\omega t + \frac{\pi}{2}\bigr) \\
\\
&=& A_0 \cos \omega t \\
\\
&=& A_0 \cos \sqrt{\frac{g}{L}} t \\
\end{eqnarray*}
となる。
周期$T$については1周期分を考えると
\begin{eqnarray*}
\omega T= 2\pi
\end{eqnarray*}
であるので、
\begin{eqnarray*}
T &=& \frac{2\pi}{\omega} \\
\\
&=& \frac{2\pi}{\sqrt{\frac{g}{L}}} \\
\\
&=& 2\pi \sqrt{\frac{L}{g}}
\end{eqnarray*}
振幅$A$は位置$x(t)$の関数より
\begin{eqnarray*}
A= A_0
\end{eqnarray*}
(3)
鉛直線を基準とすると時刻$t_1$において、$x(t_1)=0$なので
\begin{eqnarray*}
x(t_1) = A_0 \cos \omega t_1 &=& 0 \\
\\
\cos \omega t_1 &=& 0 \\
\\
\omega t_1 &=& \frac{\pi}{2} \\
\\
t_1 &=& \frac{\pi}{2\omega} \\
\\
&=& \frac{\pi}{2\sqrt{\frac{L}{g}}} \\
\\
&=& \frac{\pi}{2} \sqrt{\frac{g}{L}}\\
\end{eqnarray*}
となる。
(4)
位置$x(t)$の関数は
\begin{eqnarray*}
x(t) &=& A_0 \cos \sqrt{\frac{g}{L}} t \\
\end{eqnarray*}
であるから
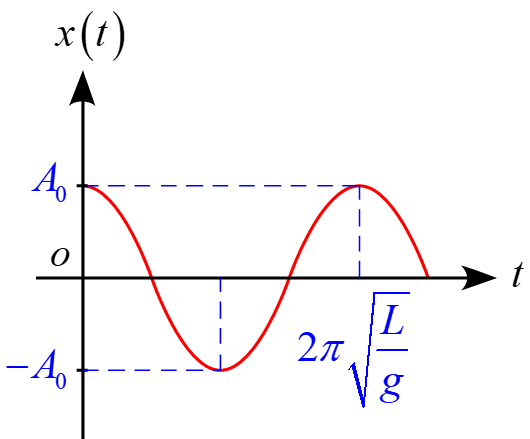
となる。