問題
質点が単振動している。1周期についての運動エネルギーの平均値$\bar{K}$と弾性力による位置エネルギーの平均値$\bar{U}$を求め、これらが等しいことを示せ。
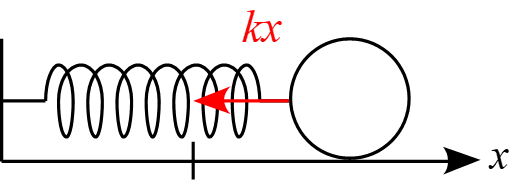
解答
図のような単振動のモデルを考えた場合、
運動方程式は
\begin{eqnarray*}
m \frac{\diff v}{\diff t} =-kx
\end{eqnarray*}
となる。
両辺を$x$で積分すると、
\begin{eqnarray*}
\int m\frac{\diff v}{\diff t}\diff x &=&\int (-kx)\ \diff x\\
\\
\int m\frac{\diff v}{\diff t}v\ \diff t &=&\int (-kx)\ \diff x\\
\\
\int\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2\right)\diff t
&=&\int \frac{\diff}{\diff x}\left(-\frac{1}{2}kx^2\right)\diff x\\
\end{eqnarray*}
となります。
この式が、この運動モデルの「仕事とエネルギーの関係式」を表しています。

さらに変形すると
\begin{eqnarray*}
\int\frac{\diff}{\diff t}\left(\frac{1}{2}mv^2\right)\diff t
+ \int \frac{\diff}{\diff x}\left(\frac{1}{2}kx^2\right)\diff x&=& 0
\end{eqnarray*}
となります。左辺第一項は「運動エネルギー$K(t)$の変化量$\Delta K$」を表し、左辺第二項は「弾性力による位置エネルギー$U(t)$」を表しています。

従って、運動エネルギー$K(t)$と位置エネルギー$U(t)$は
\begin{eqnarray*}
K(t) &=& \frac{1}{2}mv^2 \\
\\
U(t) &=& \frac{1}{2}kx^2 \\
\end{eqnarray*}
で表されます。
ここで、位置$x(t)$と速度$v(t)$は単振動の運動方程式の一般解より
\begin{eqnarray*}
x(t) &=& A \sin (\omega t + \phi) \\
\\
v(t) &=& \frac{\diff x(t)}{\diff t}= A \omega \cos (\omega t + \phi) \\
\end{eqnarray*}
と表されます。
従って、運動エネルギー$K(t)$と位置エネルギー$U(t)$は
\begin{eqnarray*}
K(t) = \frac{1}{2}mv^2 &=& \frac{1}{2}m [A \omega \cos (\omega t + \phi)]^2\\
\\
&=& \frac{1}{2}m A^2 \omega^2 \cos^2 (\omega t + \phi) \\
\\\\
U(t) = \frac{1}{2}kx^2 &=& \frac{1}{2}k [A \sin (\omega t + \phi)]^2\\
\\
&=& \frac{1}{2}k A^2 \sin^2 (\omega t + \phi)\\
\\
&=& \frac{1}{2}m \omega^2 A^2 \sin^2 (\omega t + \phi)
\qquad(\omega^2=\frac{k}{m})
\end{eqnarray*}
となります。
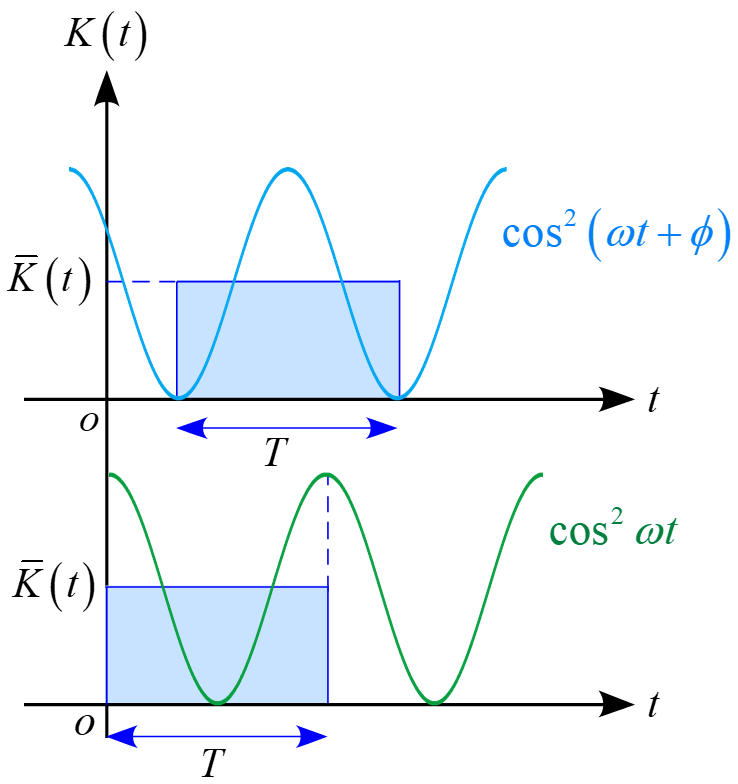
求める量は1周期分のそれぞれ平均値$\bar{k}(t), \bar{U}(t)$なので、初期位相をずらして計算すると、
\begin{eqnarray*}
\bar{k}(t) &=& \frac{1}{T} \int_0^T \frac{1}{2}m A^2 \omega^2 \cos^2 \omega t \ \diff t\\
\\
&=& \frac{1}{T} \int_0^T \frac{1}{2}m A^2 \omega^2 \frac{1}{2} (1 + cos 2\omega t) \ \diff t\\
\\
&=& \frac{mA^2\omega^2}{4T} \int_0^T (1 + cos 2\omega t) \diff t \\
\\
&=& \frac{mA^2\omega^2}{4T} \biggl[t + \frac{1}{2\omega} \sin 2\omega t \biggr]_0^T \\
\\
&=& \frac{mA^2\omega^2}{4T} \biggl[T + \frac{1}{2\omega} \sin 2\omega T - \biggl(0 + \frac{1}{2\omega} \sin 2\omega 0\biggr) \biggr] \\
\\
&=& \frac{mA^2\omega^2}{4T} T \\
\\
&=& \frac{mA^2\omega^2}{4}
\end{eqnarray*}
となり、
\begin{eqnarray*}
\bar{U}(t) &=& \frac{1}{T} \int_0^T \frac{1}{2}m A^2 \omega^2 \sin^2 \omega t \ \diff t\\
\\
&=& \frac{1}{T} \int_0^T \frac{1}{2}m A^2 \omega^2 \frac{1}{2} (1 - cos 2\omega t) \ \diff t\\
\\
&=& \frac{mA^2\omega^2}{4T} \int_0^T (1 - cos 2\omega t) \diff t \\
\\
&=& \frac{mA^2\omega^2}{4T} \biggl[t - \frac{1}{2\omega} \sin 2\omega t \biggr]_0^T \\
\\
&=& \frac{mA^2\omega^2}{4T} \biggl[T - \frac{1}{2\omega} \sin 2\omega T - \biggl(0 - \frac{1}{2\omega} \sin 2\omega 0\biggr) \biggr] \\
\\
&=& \frac{mA^2\omega^2}{4T} T \\
\\
&=& \frac{mA^2\omega^2}{4}
\end{eqnarray*}
となります。
従って、
\begin{eqnarray*}
\bar{K}(t) = \bar{K}(t) =\frac{mA^2\omega^2}{4}
\end{eqnarray*}
となります。
三角関数の次数下げ
加法定理
\begin{eqnarray*}
\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta
\end{eqnarray*}
において、$\beta = \alpha$の場合を考えると
\begin{eqnarray*}
\cos (\alpha + \alpha) &=& \cos \alpha \cos \alpha - \sin \alpha \sin \alpha \\
\\
\cos 2\alpha &=& \cos^2 \alpha - \sin^2 \alpha \\
\end{eqnarray*}
となる。
また、
\begin{eqnarray*}
\cos^2 \alpha + \sin^2 \alpha =1
\end{eqnarray*}
であるから、$\cos^2 \alpha$については
\begin{eqnarray*}
\cos^2 \alpha &=& \sin^2 \alpha + \cos 2\alpha \\
\\
\cos^2 \alpha &=& 1- \cos^2 \alpha + \cos 2\alpha \\
\\
2\cos^2 \alpha &=& 1 + \cos 2\alpha \\
\\
\cos^2 \alpha &=& \frac{1}{2}(1 + \cos 2\alpha)
\end{eqnarray*}
となる。
一方、$\sin^2 \alpha$については
\begin{eqnarray*}
\sin^2 \alpha &=& \cos^2 \alpha - \cos 2\alpha \\
\\
\sin^2 \alpha &=& 1- \sin^2 \alpha - \cos 2\alpha \\
\\
2\sin^2 \alpha &=& 1 - \cos 2\alpha \\
\\
\sin^2 \alpha &=& \frac{1}{2}(1 - \cos 2\alpha)
\end{eqnarray*}
となる。