問題
ある高さから質量$m$の物体を真下に投げ下ろしところ、地表に衝突する瞬間の速度の大きさが$v_1$となった。
(1) この衝突において力$F$が作用したとする。地表に衝突した瞬間の運動を記述せよ。
(2) この衝突において、力$F$は重力$mg$に比べて十分に大きく$F \gg mg$であり、又、衝突は完全弾性衝突であったとする。物体が地表から受けた力積$I$を運動方程式から導け。
解答
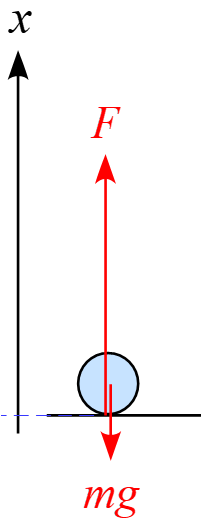
(1)
衝突した瞬間に作用する力は、場の力「重力 $mg$」と接触力「地表から受ける力$F$(抗力を含む)」なので、上向きを正に軸を設定したとすると、
\begin{eqnarray*}
ma = F-mg
\end{eqnarray*}
と表すことができる。
(2)
運動方程式は
\begin{eqnarray*}
ma &=& F-mg \\
\\
ma &=& F \biggl( 1- \frac{mg}{F} \biggr)
\end{eqnarray*}
である。ここで$F \gg mg$より$1 \gg \frac{mg}{F}$なので
\begin{eqnarray*}
ma = F
\end{eqnarray*}
と近似できる。
問いでは、力積$I$を導くことを目的としているので、この運動方程式を時間$t$で積分すればよい。
従って、
\begin{eqnarray*}
ma &=& F \\
\\
m \frac{\diff v}{\diff t}&=& F \\
\\
\int m \frac{\diff v}{\diff t} \diff t &=& \int F \diff t \\
\\
\int \frac{\diff }{\diff t} \bigl( mv \bigr) \diff t &=& \int F \diff t \\
\end{eqnarray*}
となる。この式がこの衝突の「力積と運動量の関係式」になる。

ここで衝突の前後での速度は軸を上向きに設定したので
\begin{eqnarray*}
衝突直前:\ v(t_1) &=& -v_1 \\
\\
衝突直後:\ v(t'_1) &=&v'_1 = v_1
\end{eqnarray*}
とすると、図の様になる。
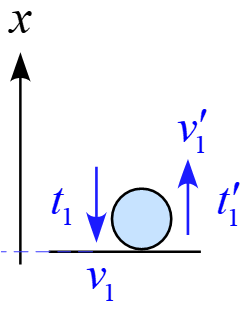
従って、この衝突の前後での積分区間を指定すると
\begin{eqnarray*}
\int_{t_1}^{t'_1} \frac{\diff }{\diff t} \bigl( mv \bigr) \diff t &=& \int_{t_1}^{t'_1} F \diff t \\
\\
\bigl[ mv \bigr]_{v(t_1)}^{v(t'_1)} &=& \int_{t_1}^{t'_1} F \diff t \\
\\
mv(t'_1) - mv(t_1) &=& \int_{t_1}^{t'_1} F \diff t \\
\\
mv_1 - m(-v_1)&=& \int_{t_1}^{t'_1} F \diff t \\
\\
2mv_1&=& \int_{t_1}^{t'_1} F \diff t \\
\\
2mv_1 &=& I\\
\end{eqnarray*}
となる。