問題
軽い棒の両端に質量$m$の物体と質量$M$の物体が図の様に取り付けられ、点$o$で糸に吊るされている。
この棒が回転しない条件を以下の問題に沿って答えよ。
(1) 棒に作用する力を書き込め。
(2) 棒の運動方程式を記述せよ。
(3) 棒の回転の運動方程式を記述せよ。
(4) 棒が回転しない条件$\displaystyle \frac{r_1}{r_2}$を求めよ。
解答
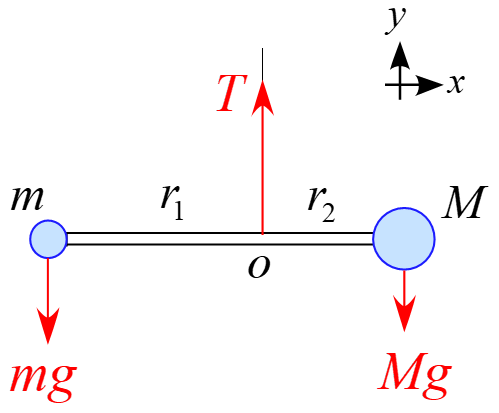
(1)
軸の設定は「$x$軸は右向き正」とし「$y$軸は上向き正」とします。
棒に作用する力は、左右の重り「重力$mg$」「重力$Mg$」と「糸の張力$T$」の3つの力が作用することになります。
(2)
運動方程式は
\begin{eqnarray*}
(m+M) a_y = T-mg -Mg
\end{eqnarray*}
となり、$a_y=0 \ $(動かない)より
\begin{eqnarray*}
0 = T-mg -Mg
\end{eqnarray*}
となります。
(3)
回転の運動方程式は「$\displaystyle \frac{\diff \vec{L}}{\diff t}=\vec{M}$」と表され、また、力のモーメント$\vec{M}$は位置ベクトル$\vec{r}$と作用する力$\vec{F}$の外積で表されるので、$\vec{r}, \vec{F}$を図の様に設定します。
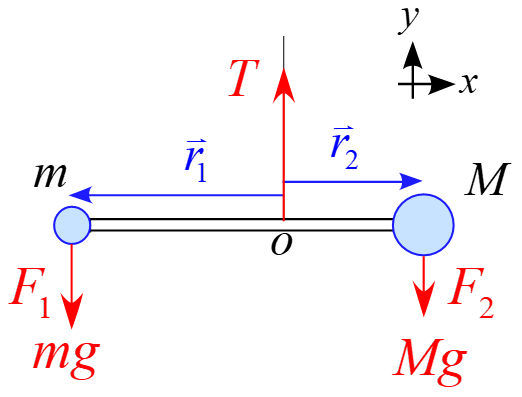
$\vec{r}, \vec{F}$の成分は
\begin{eqnarray*}
\vec{r}_{1} =
\left(
\begin{array}{c}
-r_1 \\
0 \\
0
\end{array}
\right) , \quad
\vec{r}_{2} =
\left(
\begin{array}{c}
r_2 \\
0 \\
0
\end{array}
\right)
\end{eqnarray*}
\begin{eqnarray*}
\vec{F}_{1} =
\left(
\begin{array}{c}
0 \\
-mg \\
0
\end{array}
\right) , \quad
\vec{F}_{2} =
\left(
\begin{array}{c}
0 \\
-Mg \\
0
\end{array}
\right)
\end{eqnarray*}
となるので、左右の重りによる力のモーメント$\vec{M}_1, \vec{M}_2$は
\begin{eqnarray*}
\vec{M}_1 = \vec{r}_1 \times \vec{F}_1 &= &
\left(
\begin{array}{c}
-r_1 \\
0 \\
0
\end{array}
\right) \times
\left(
\begin{array}{c}
0 \\
-mg \\
0
\end{array}
\right) =
\left(
\begin{array}{c}
0 \cdot 0 - 0 \cdot (-mg) \\
0 \cdot 0 - (-r_1) \cdot 0 \\
-r_1 \cdot (-mg) - 0 \cdot 0
\end{array}
\right) \\
\\
&= &
\left(
\begin{array}{c}
0 \\
0 \\
r_1 mg
\end{array}
\right) \\
\\
\vec{M}_2 = \vec{r}_2 \times \vec{F}_2 &= &
\left(
\begin{array}{c}
r_2 \\
0 \\
0
\end{array}
\right) \times
\left(
\begin{array}{c}
0 \\
-Mg \\
0
\end{array}
\right) =
\left(
\begin{array}{c}
0 \cdot 0 - 0 \cdot (-Mg) \\
0 \cdot 0 - r_2 \cdot 0 \\
r_2 \cdot (-Mg) - 0 \cdot 0
\end{array}
\right) \\
\\
&= &
\left(
\begin{array}{c}
0 \\
0 \\
-r_2 Mg
\end{array}
\right) \\
\end{eqnarray*}
となります。
従って、回転の運動方程式は
\begin{eqnarray*}
\frac{\diff \vec{L}}{\diff t} = \vec{M} = \vec{M}_1 + \vec{M}_2 &=&
\left(
\begin{array}{c}
0 \\
0 \\
r_1 mg
\end{array}
\right) +
\left(
\begin{array}{c}
0 \\
0 \\
-r_2 Mg
\end{array}
\right) \\
\\
&=&
\left(
\begin{array}{c}
0 \\
0 \\
r_1 mg - r_2 Mg
\end{array}
\right)
\end{eqnarray*}
となるので、
\begin{eqnarray*}
\frac{\diff \vec{L}}{\diff t} =
\left(
\begin{array}{c}
\frac{\diff L_x}{\diff t} \\
\\
\frac{\diff L_y}{\diff t} \\
\\
\frac{\diff L_z}{\diff t}
\end{array}
\right) =
\left(
\begin{array}{c}
0 \\
0 \\
r_1 mg - r_2 Mg
\end{array}
\right) \\
\end{eqnarray*}
となります。この式がこの運動における「(力の)モーメントと角運動量の関係式」になります。
注)
張力$T$に対する力のモーメントは支点から力の作用点の距離がゼロなので考慮しなくても良い。

(4)
棒が回転しない条件は$\displaystyle \frac{\diff \vec{L}}{\diff t}=0$、即ち、$\displaystyle \frac{\diff L_z}{\diff t}=0$であれば良いので
\begin{eqnarray*}
\frac{\diff L_z}{\diff t} = r_1 mg - r_2 Mg &=& 0 \\
\\
r_1 mg &=& r_2 Mg \\
\\
\frac{r_1}{r_2} &=& \frac{M}{m}
\end{eqnarray*}
となります。